
若数列 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 都有
都有 ,记
,记 .
.
(1)求 ,
, 的值;
的值;
(2)求数列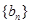 的通项公式;
的通项公式;
(3)若 求证:对任意
求证:对任意 .
.
(1)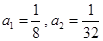 ;(2)
;(2)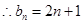 ;(3)见试题解析.
;(3)见试题解析.
【解析】
试题分析:(1)分别令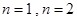 可求得
可求得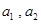 的值;(2)利用
的值;(2)利用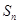 与
与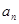 的关系式,先求
的关系式,先求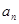 ,再利用已知条件
,再利用已知条件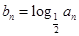 求得数列
求得数列 的通项公式;(3)先利用累加法求得
的通项公式;(3)先利用累加法求得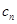 ,再利用裂项相消法求和
,再利用裂项相消法求和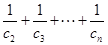 ,进而可证明不等式.
,进而可证明不等式.
试题解析:(1)由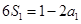 ,得
,得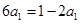 ,解得
,解得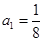 . 1分
. 1分
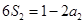 ,得
,得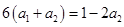 ,解得
,解得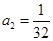 .
3分
.
3分
(2)由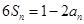 ①,
①,
当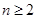 时,有
时,有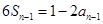 ②,
4分
②,
4分
①-②得: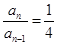 ,
5分
,
5分
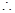 数列
数列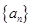 是首项
是首项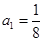 ,公比
,公比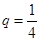 的等比数列 6分
的等比数列 6分
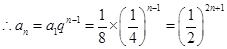 , 7分
, 7分
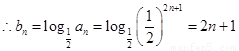 . 8分
. 8分
(3)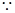
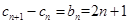 ,
,
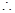
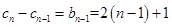 , (1)
, (1)
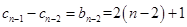 , (2)
, (2)
,
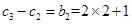 ,
,
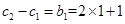 , (
, (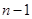 ) 9分
) 9分
(1)+(2)+ +(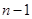 )得
)得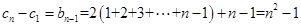 , 10分
, 10分
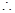
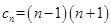 ,
11分
,
11分
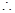
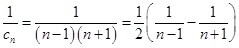 ,
12分
,
12分
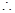
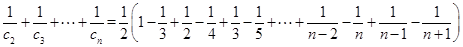
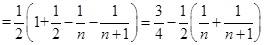 , 13分
, 13分
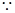
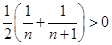 ,
,
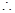
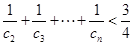 对任意
对任意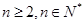 均成立. 14分
均成立. 14分
考点:1、数列通项公式的求法;2、数列前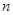 项和的求法;3、数列不等式的证明.
项和的求法;3、数列不等式的证明.


科目:高中数学 来源: 题型:
(本小题满分14分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的正整数
,对任意的正整数![]() ,都有
,都有![]() 成立,记
成立,记![]() 。
。
(Ⅰ)求数列![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)记![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对任意正整数
,求证:对任意正整数![]() 都有
都有![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点![]()
![]() )都在函数
)都在函数![]() 的图象上.
的图象上.
(1)若数列![]() 是等差数列,求证数列
是等差数列,求证数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 的前
的前![]() 项和为
项和为![]() =
=![]() ,过点
,过点![]() 的直线与两坐标轴所围成三角 形面积为
的直线与两坐标轴所围成三角 形面积为![]() ,求使
,求使![]() 对
对![]()
![]() 恒成立的实数
恒成立的实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届广东省广州市海珠区高三入学摸底考试理科数学试卷(解析版) 题型:解答题
若数列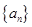 的前
的前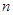 项和为
项和为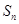 ,对任意正整数
,对任意正整数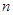 都有
都有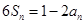 ,记
,记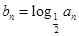 .
.
(1)求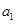 ,
,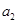 的值;
的值;
(2)求数列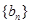 的通项公式;
的通项公式;
(3)若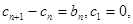 求证:对任意
求证:对任意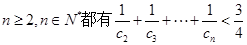 .
.
查看答案和解析>>
科目:高中数学 来源:江苏省扬州中学09-10学年高二下学期期中考试(文科) 题型:解答题
设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 在函数
在函数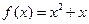 的图象上.
的图象上.
(1)求a1,a2,a3值,并求 的表达式;
的表达式;
(2)将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),(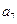 ,
,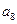 ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
,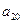 );(
);( ),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;w*w^w.k&s#5@u.c~o*m
的值;w*w^w.k&s#5@u.c~o*m
(3)设 为数列
为数列 的前
的前 项积,是否存在实数
项积,是否存在实数 ,使得不等式
,使得不等式 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com