
،¾جâؤ؟،؟بçح¼تاز»¸ِ°ë¾¶خھ2ا§أ×£¬ش²ذؤ½اخھ![]() µؤةبذخسخہہاّµؤئ½أوت¾زâح¼
µؤةبذخسخہہاّµؤئ½أوت¾زâح¼![]() تا°ë¾¶
تا°ë¾¶![]() ةدز»µم£¬
ةدز»µم£¬![]() تاش²»،
تاش²»،![]() ةدز»µم£¬از
ةدز»µم£¬از![]() .دضشعدك¶خ
.دضشعدك¶خ![]() £¬دك¶خ
£¬دك¶خ![]() ¼°ش²»،
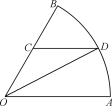
¼°ش²»،![]() ب¶خثùت¾خ»ضأةèء¢¹م¸وخ»£¬¾²âثم¹م¸وخ»³ِ×âتصبëتا£؛دك¶خ
ب¶خثùت¾خ»ضأةèء¢¹م¸وخ»£¬¾²âثم¹م¸وخ»³ِ×âتصبëتا£؛دك¶خ![]() ´¦أ؟ا§أ×خھ
´¦أ؟ا§أ×خھ![]() شھ£¬دك¶خ
شھ£¬دك¶خ![]() ¼°ش²»،
¼°ش²»،![]() ´¦أ؟ا§أ×¾ùخھ
´¦أ؟ا§أ×¾ùخھ![]() شھ£®ةè
شھ£®ةè![]() »،¶ب£¬¹م¸وخ»³ِ×âµؤ×ـتصبëخھ
»،¶ب£¬¹م¸وخ»³ِ×âµؤ×ـتصبëخھ![]() شھ£®
شھ£®
(1)اَ![]() ¹طسع
¹طسع![]() µؤ؛¯ت½âخِت½£¬²¢ض¸³ِ¸أ؛¯تµؤ¶¨زهسٍ£»
µؤ؛¯ت½âخِت½£¬²¢ض¸³ِ¸أ؛¯تµؤ¶¨زهسٍ£»
(2)تشخت£؛![]() خھ؛خضµت±£¬¹م¸وخ»³ِ×âµؤ×ـتصبë×î´َ£؟²¢اَ³ِئن×î´َضµ£®
خھ؛خضµت±£¬¹م¸وخ»³ِ×âµؤ×ـتصبë×î´َ£؟²¢اَ³ِئن×î´َضµ£®
،¾´ً°¸،؟£¨1£©![]() £»£¨2£©µ±
£»£¨2£©µ±![]() ت±£¬¹م¸وخ»³ِ×âµؤ×ـتصبë×î´َ£¬×î´َضµخھ
ت±£¬¹م¸وخ»³ِ×âµؤ×ـتصبë×î´َ£¬×î´َضµخھ![]() شھ.
شھ.
،¾½âخِ،؟
£¨1£©¸ù¾فجâز⣬ہûسأصدز¶¨ہياَµأOCµؤضµ£¬شظاَ»،³¤DB£¬اَ³ِ؛¯تyµؤ½âخِت½£¬ذ´³ِxµؤب،ضµ·¶خ§£»
£¨2£©اَ؛¯تyµؤµ¼ت£¬ہûسأµ¼تإذ¶د؛¯تµؤµ¥µ÷ذش£¬اَ³ِ؛¯تµؤ×îضµ؛ح¶شس¦xµؤضµ£®
(1)زٍخھ![]() £¬ثùزش
£¬ثùزش![]() .
.
شع![]() ضذ£¬
ضذ£¬![]() £¬
£¬![]() £¬
£¬![]() .
.
سةصدز¶¨ہي£¬µأ![]() £¬
£¬
µأ![]() £¬
£¬![]() .
.
سضش²»،![]() ³¤خھ
³¤خھ![]() £¬
£¬
ثùزش![]()
![]() .
.
(2)¼ا![]() £¬
£¬
شٍ![]() £¬
£¬
ءî![]() £¬µأ
£¬µأ![]() .
.
µ±![]() ±ن»¯ت±£¬
±ن»¯ت±£¬![]() £¬
£¬![]() µؤ±ن»¯بçدآ±ي£؛
µؤ±ن»¯بçدآ±ي£؛
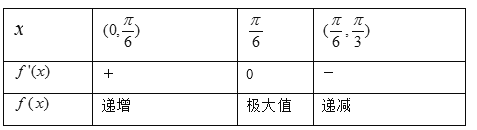
ثùزش![]() شع
شع![]() ´¦ب،µأ¼«´َضµ£¬صâ¸ِ¼«´َضµ¾حتا×î´َضµ£¬¼´
´¦ب،µأ¼«´َضµ£¬صâ¸ِ¼«´َضµ¾حتا×î´َضµ£¬¼´![]() .
.
¹تµ±![]() ت±£¬¹م¸وخ»³ِ×âµؤ×ـتصبë×î´َ£¬×î´َضµخھ
ت±£¬¹م¸وخ»³ِ×âµؤ×ـتصبë×î´َ£¬×î´َضµخھ![]() شھ£®
شھ£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھحضش²![]() £؛
£؛ ![]() ¹µم
¹µم![]() £¬ہëذؤآتخھ
£¬ہëذؤآتخھ![]() .
.
£¨1£©اَحضش²![]() µؤ·½³ج£»
µؤ·½³ج£»
£¨2£©![]() £¬
£¬ ![]() تا¹µم
تا¹µم![]() از»¥دà´¹ض±µؤء½جُض±دك£¬ئنضذ
از»¥دà´¹ض±µؤء½جُض±دك£¬ئنضذ![]() ½»ش²
½»ش²![]() سع
سع![]() £¬
£¬ ![]() ء½µم£¬
ء½µم£¬ ![]() ½»حضش²
½»حضش²![]() سعءيز»¸ِµم
سعءيز»¸ِµم![]() £¬اَ
£¬اَ![]() أو»ب،µأ×î´َضµت±ض±دك
أو»ب،µأ×î´َضµت±ض±دك![]() µؤ·½³ج.
µؤ·½³ج.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ضضة豸ثو×إت¹سأؤêدقµؤشِ¼س£¬أ؟ؤêµؤخ¬»¤·ردàس¦شِ¼س![]() دض¶شز»إْ¸أة豸½ّذذµ÷²é£¬µأµ½صâإْة豸×ش¹؛بëت¹سأض®بصئً£¬ا°خهؤêئ½¾ùأ؟ج¨ة豸أ؟ؤêµؤخ¬»¤·رسأ´َضآبç±ي£؛
دض¶شز»إْ¸أة豸½ّذذµ÷²é£¬µأµ½صâإْة豸×ش¹؛بëت¹سأض®بصئً£¬ا°خهؤêئ½¾ùأ؟ج¨ة豸أ؟ؤêµؤخ¬»¤·رسأ´َضآبç±ي£؛
ؤê·ف | 1 | 2 | 3 | 4 | 5 |
خ¬»¤·ر |
|
|
|
|
|
![]() ¢ٌ
¢ٌ![]() اَy¹طسعtµؤدكذش»ط¹é·½³ج£»
اَy¹طسعtµؤدكذش»ط¹é·½³ج£»
![]() ¢ٍ
¢ٍ![]() بô¸أة豸µؤ¼غ¸ٌتاأ؟ج¨5حٍشھ£¬¼×بدخھس¦¸أت¹سأآْخهؤê»»ز»´خة豸£¬¶ّززشٍبدخھس¦¸أت¹سأآْت®ؤê»»ز»´خة豸£¬ؤمبدخھ¼×؛حززث¸üسذµہہي£؟²¢ثµأ÷ہيسة£®
بô¸أة豸µؤ¼غ¸ٌتاأ؟ج¨5حٍشھ£¬¼×بدخھس¦¸أت¹سأآْخهؤê»»ز»´خة豸£¬¶ّززشٍبدخھس¦¸أت¹سأآْت®ؤê»»ز»´خة豸£¬ؤمبدخھ¼×؛حززث¸üسذµہہي£؟²¢ثµأ÷ہيسة£®
![]() ²خ؟¼¹«ت½£؛
²خ؟¼¹«ت½£؛ £¬
£¬![]()
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھµمA£¨t£¬1£©خھ؛¯تy£½ax2+bx+4£¨a£¬bخھ³£ت£¬ازa،ظ0£©سëy£½xح¼دَµؤ½»µم£®
£¨1£©اَt£»
£¨2£©بô؛¯تy£½ax2+bx+4µؤح¼دَسëxضلض»سذز»¸ِ½»µم£¬اَa£¬b£»
£¨3£©بô1،ـa،ـ2£¬ةèµ±![]() ،ـx،ـ2ت±£¬؛¯تy£½ax2+bx+4µؤ×î´َضµخھm£¬×îذ،ضµخھn£¬اَm©پnµؤ×îذ،ضµ£®
،ـx،ـ2ت±£¬؛¯تy£½ax2+bx+4µؤ×î´َضµخھm£¬×îذ،ضµخھn£¬اَm©پnµؤ×îذ،ضµ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ؛¯ت![]()
£¨1£©بô؛¯ت![]() شع
شع![]() ةدµ¥µ÷µف¼ُ£¬اَتµت
ةدµ¥µ÷µف¼ُ£¬اَتµت![]() µؤب،ضµ·¶خ§£»
µؤب،ضµ·¶خ§£»
£¨2£©تا·ٌ´وشعتµت![]() £¬ت¹µأ
£¬ت¹µأ![]() شع
شع![]() ةدµؤضµسٍا،؛أتا
ةدµؤضµسٍا،؛أتا![]() £؟بô´وشع£¬اَ³ِتµت
£؟بô´وشع£¬اَ³ِتµت![]() µؤضµ£»بô²»´وشع£¬ثµأ÷ہيسة.
µؤضµ£»بô²»´وشع£¬ثµأ÷ہيسة.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ئَزµ2017ؤêµؤ´؟ہûبَخھ500حٍشھ£¬زٍة豸ہد»¯µبشزٍ£¬ئَزµµؤةْ²ْؤـء¦ضًؤêدآ½µ£¬بô²»ؤـ½ّذذ¼¼تُ¸ؤشى£¬ش¤²â´س2018ؤêئًأ؟ؤê±بةدز»ؤê´؟ہûبَ¼ُةظ20حٍشھ£¬2018ؤê³ُ¸أئَزµز»´خذشح¶بë×ت½ً600حٍشھ½ّذذ¼¼تُ¸ؤشى£¬ش¤²âشعخ´؟غ³¼¼تُ¸ؤشى×ت½ًµؤاé؟ِدآ£¬µع![]() ؤ꣨زش2018ؤêخھµعز»ؤ꣩µؤہûبَخھ
ؤ꣨زش2018ؤêخھµعز»ؤ꣩µؤہûبَخھ![]() حٍشھ£¨
حٍشھ£¨![]() خھصصûت£©.
خھصصûت£©.
£¨1£©ةè´س½ٌؤêئًµؤا°![]() ؤ꣬بô¸أئَزµ²»½ّذذ¼¼تُ¸ؤشىµؤہغ¼ئ´؟ہûبَخھ
ؤ꣬بô¸أئَزµ²»½ّذذ¼¼تُ¸ؤشىµؤہغ¼ئ´؟ہûبَخھ![]() حٍشھ£¬½ّذذ¼¼تُ¸ؤشى؛َµؤہغ¼ئ´؟ہûبَخھ
حٍشھ£¬½ّذذ¼¼تُ¸ؤشى؛َµؤہغ¼ئ´؟ہûبَخھ![]() حٍشھ£¨ذë؟غ³¼¼تُ¸ؤشى×ت½ً£©£¬اَ
حٍشھ£¨ذë؟غ³¼¼تُ¸ؤشى×ت½ً£©£¬اَ![]() £¬
£¬![]() µؤ±ي´ïت½£»
µؤ±ي´ïت½£»
£¨2£©زہةدتِش¤²â£¬´س2018ؤêئً¸أئَزµضءةظ¾¹¶àةظؤ꣬½ّذذ¼¼تُ¸ؤشى؛َµؤہغ¼ئہûبَ³¬¹²»½ّذذ¼¼تُ¸ؤشىµؤہغ¼ئ´؟ہûبَ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ؛¯ت![]() £¬
£¬ ![]() £¨
£¨![]() خھ³£ت£©£®
خھ³£ت£©£®
£¨1£©بô؛¯ت![]() سë؛¯ت
سë؛¯ت![]() شع
شع![]() ´¦سذدàح¬µؤاذدك£¬اَتµت
´¦سذدàح¬µؤاذدك£¬اَتµت![]() µؤضµ£»
µؤضµ£»
£¨2£©بô![]() £¬از
£¬از![]() £¬ض¤أ÷£؛
£¬ض¤أ÷£؛ ![]() £»
£»
£¨3£©بô¶شبخزâ![]() £¬²»µبت½؛م
£¬²»µبت½؛م![]() ³ةء¢£¬اَتµت
³ةء¢£¬اَتµت![]() µؤب،ضµ·¶خ§£®
µؤب،ضµ·¶خ§£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھµمP£¨x0£¬y0£©£¨x0،ظ![]() £©شعحضش²C£؛
£©شعحضش²C£؛![]() £¨a£¾b£¾0£©ةد£¬بôµمMخھحضش²Cµؤسز¶¥µم£¬ازPO،حPM £¨Oخھ×ّ±êشµم£©£¬شٍحضش²Cµؤہëذؤآتeµؤب،ضµ·¶خ§تا
£¨a£¾b£¾0£©ةد£¬بôµمMخھحضش²Cµؤسز¶¥µم£¬ازPO،حPM £¨Oخھ×ّ±êشµم£©£¬شٍحضش²Cµؤہëذؤآتeµؤب،ضµ·¶خ§تا
A. £¨0£¬![]() £© B. £¨0£¬1£© C. £¨
£© B. £¨0£¬1£© C. £¨![]() £¬1£© D. £¨0£¬
£¬1£© D. £¨0£¬![]() £©
£©
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ¶¨زهشع![]() ةدµؤئو؛¯ت
ةدµؤئو؛¯ت![]() آْ×م
آْ×م![]() £¬
£¬ ![]() خھتءذ
خھتءذ![]() µؤا°
µؤا°![]() دî؛ح£¬از
دî؛ح£¬از![]() £¬شٍ
£¬شٍ![]() __________£®
__________£®
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com