

 =x,则
=x,则 =1-x,0<x<1.根据矩形EFGH的面积为 EH•EF=x(1-x)ab,可得当x=
=1-x,0<x<1.根据矩形EFGH的面积为 EH•EF=x(1-x)ab,可得当x= 时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大,从而得出结论.
时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大,从而得出结论. =x,则
=x,则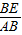 =1-x,0<x<1.
=1-x,0<x<1. 时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大.
时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
 如图所示:一块矩形的太阳能吸光板安装在三棱锥形状的支撑架上,矩形EFGH的四个顶点分别在边AB、BC、CD、AD上,已知AC=a,BD=b,问E、F、G、H在什么位置时吸光板的吸光量最大?
如图所示:一块矩形的太阳能吸光板安装在三棱锥形状的支撑架上,矩形EFGH的四个顶点分别在边AB、BC、CD、AD上,已知AC=a,BD=b,问E、F、G、H在什么位置时吸光板的吸光量最大?查看答案和解析>>
科目:高中数学 来源: 题型:
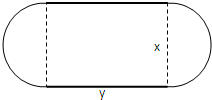 某学校拟建一块周长为400米的操场(如图所示),操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域.
某学校拟建一块周长为400米的操场(如图所示),操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示:一块矩形的太阳能吸光板安装在三棱锥形状的支撑架上,矩形EFGH的四个顶点分别在边AB、BC、CD、AD上,已知AC=a,BD=b,问E、F、G、H在什么位置时吸光板的吸光量最大?
如图所示:一块矩形的太阳能吸光板安装在三棱锥形状的支撑架上,矩形EFGH的四个顶点分别在边AB、BC、CD、AD上,已知AC=a,BD=b,问E、F、G、H在什么位置时吸光板的吸光量最大?查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省池州一中高二(上)期中数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com