
分析 设上底边长为b,确定第n次,得到的梯形上底边长为an,利用重复1975次,最后得到的梯形上底边长恰好与原来的梯形上底边长相等,求出b,即可求原梯形的面积.
解答 解:设上底边长为b,第n次,得到的梯形上底边长为an,a1=$\frac{1}{2}$(b-a)
则2an=b-an-1,
∴2(an-$\frac{1}{3}$b)=-(an-1-$\frac{1}{3}$b),
∴an-$\frac{1}{3}$b=$\frac{b-3a}{6}•(-\frac{1}{2})^{n-1}$
∴an=$\frac{b-3a}{6}•(-\frac{1}{2})^{n-1}$+$\frac{1}{3}$b
∵重复1975次,最后得到的梯形上底边长恰好与原来的梯形上底边长相等,
∴$\frac{b-3a}{6}•(-\frac{1}{2})^{n-1}$+$\frac{1}{3}$b=a
∴$\frac{b-3a}{6}•(-\frac{1}{2})^{1974}$=$\frac{3a-b}{3}$,
∴b=3a,
∴原梯形的面积$\frac{a+3a}{2}•h$=2ah.
点评 本题考查归纳推理,考查数列的通项,考查学生的计算能力,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
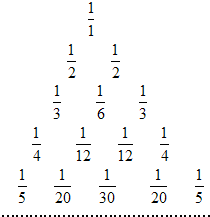 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,| A. | $\frac{1}{2016×2015×2014}$ | B. | $\frac{1}{2016×2017}$ | C. | $\frac{1}{2016×2015×1006}$ | D. | $\frac{1}{2016×2015×1007}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -6 | C. | -5 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com