
【题目】某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形![]() 挖去扇形
挖去扇形![]() 后构成的).已知
后构成的).已知![]() ,线段
,线段![]() 与弧
与弧![]() 、弧
、弧![]() 的长度之和为
的长度之和为![]() 米,圆心角为
米,圆心角为![]() 弧度.
弧度.

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)记铭牌的截面面积为![]() ,试问
,试问![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】1970年4月24日,我国发射了自己的第一颗人造地球卫星“东方红一号”,从此我国开启了人造卫星的新篇章,人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() ,
,![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
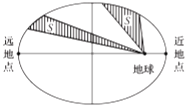
A.卫星向径的最小值为![]()
B.卫星向径的最大值为![]()
C.卫星向径的最小值与最大值的比值越小,椭圆轨道越扁
D.卫星运行速度在近地点时最小,在远地点时最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象的对称轴之间的最短距离为
的图象的对称轴之间的最短距离为![]() ,且经过点
,且经过点![]() .
.
(1)写出函数![]() 的解析式;
的解析式;
(2)若对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求实数![]() 和正整数
和正整数![]() ,使得
,使得![]() 在
在![]() 上恰有2017个零点.
上恰有2017个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 的圆心与椭圆C的上顶点重合,点P的纵坐标为
的圆心与椭圆C的上顶点重合,点P的纵坐标为![]() .
.
(1)求椭圆C的标准方程;
(2)若斜率为2的直线l与椭圆C交于A,B两点,探究:在椭圆C上是否存在一点Q,使得![]() ,若存在,求出点Q的坐标;若不存在,请说明理由.
,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,![]() ·
·![]() =0,|
=0,|![]() |=12,|
|=12,|![]() |=15,l为线段BC的垂直平分线,l与BC交于点D,E为l上异于D的任意一点.
|=15,l为线段BC的垂直平分线,l与BC交于点D,E为l上异于D的任意一点.
(1)求![]() ·
·![]() 的值;
的值;
(2)判断![]() ·
·![]() 的值是否为一个常数,并说明理由.
的值是否为一个常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若α是第一象限角,则sinα+cosα的值与1的大小关系是( )
A. sinα+cosα>1B. sinα+cosα=1C. sinα+cosα<1D. 不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为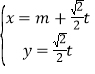 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在区间
在区间![]() 上的图像如图所示,将该函数图像上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移
上的图像如图所示,将该函数图像上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移![]() 个单位长度后,所得到的图像关于直线
个单位长度后,所得到的图像关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com