
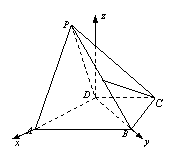
(08年新建二中二模)如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)求二面角![]() 的大小.
的大小.
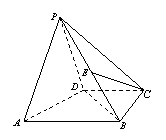
解析: 解![]() :(Ⅰ)如图,取
:(Ⅰ)如图,取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() .∵
.∵![]() 是
是![]() 的中点,
的中点,
∴![]() 且
且![]() .又∵
.又∵![]() ,
, ![]() ,
,
∴![]() 且
且![]() .∴四边形
.∴四边形![]() 是平行四边形,故得
是平行四边形,故得![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() .∵平面
.∵平面![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() .∴
.∴![]() 是
是![]() 在平面
在平面![]() 内的射影,∴
内的射影,∴![]() 是
是![]() 与平面
与平面![]() 所成的角.由已知
所成的角.由已知![]() ,∴四边形
,∴四边形![]() 是直角梯形,
是直角梯形,![]() . 设
. 设![]() ,则BD=
,则BD=![]() ,在
,在![]() 中,易得
中,易得![]() ,∴
,∴![]() ,
,![]()
![]() .又∵
.又∵![]() ,∴
,∴![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
∴![]() .
.
∴在![]() 中,
中,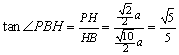 .
.
(Ⅲ)在平面![]() 内过点
内过点![]() 作
作![]() 的垂线交于
的垂线交于![]() 于
于![]() 点,连结
点,连结![]() ,则
,则![]() 是
是![]() 在平面
在平面![]() 内的射影,故
内的射影,故![]() ,∴
,∴![]() 是二面角
是二面角![]() 的平面角,由
的平面角,由![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() .在
.在![]() 中,
中,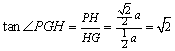 .
.
∴二面角![]() 的大小为
的大小为![]() .
.
解![]() :(Ⅰ)同解
:(Ⅰ)同解![]() .
.
(Ⅱ)设![]() ,同解
,同解![]() 中的(Ⅱ)可得
中的(Ⅱ)可得![]() .如图,以
.如图,以![]() 点为原
点为原
点,![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 点且垂直于
点且垂直于
平面![]() 的直线与
的直线与![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.![]() .
.
则![]() ,P
,P![]() ,则
,则![]() .
.
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() .可得
.可得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,∴
,∴![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() .
.
(Ⅲ)易知![]() ,则
,则![]() .设平面
.设平面![]() 的一个法向量
的一个法向量![]() ,
,
则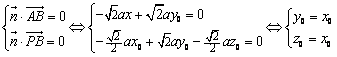 .令
.令![]() ,可得
,可得![]() .∴
.∴![]() ,故二面角
,故二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
(08年新建二中二模)已知曲线![]() :
:![]() ,过
,过![]() 上一点
上一点![]() 作一斜率为
作一斜率为![]() 的直线交曲线
的直线交曲线![]() 于另一点
于另一点![]() ,点列
,点列![]() 的横坐标构成数列
的横坐标构成数列![]() ,其中
,其中![]() .
.
⑴求![]() 与
与![]() 的关系式;
的关系式;
⑵求证:![]() 是等比数列;
是等比数列;
⑶求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年新建二中二模理)小张有一只放在![]() 个红球,
个红球,![]() 个黄球,
个黄球,![]() 个白球的箱子,且
个白球的箱子,且![]() .小刘有一只放有
.小刘有一只放有![]() 个红球,
个红球,![]() 黄球,
黄球,![]() 个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同 色时小张胜,异色时小刘胜.
个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同 色时小张胜,异色时小刘胜.
⑴用![]() 表示小张获胜的概率;
表示小张获胜的概率;
⑵若又规定当小张取红、黄、白球而胜得分分别为![]() 分、
分、![]() 分、
分、![]() 分,否则得
分,否则得![]() 分,求小张得分的期望的最大值及此时
分,求小张得分的期望的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年新建二中二模文)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为![]() ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验一粒种子,假定某次实验种子发芽则称该次实验 是成功的,如果种子没有发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验一粒种子,假定某次实验种子发芽则称该次实验 是成功的,如果种子没有发芽,则称该次实验是失败的.
⑴第一小组做了三次实验,求至少有两次实验成功的概率;
⑵第二小组进行试验,到成功了![]() 次为止,求在第四次成功之前共有三次失败,且恰有两次连续 失败的概率.
次为止,求在第四次成功之前共有三次失败,且恰有两次连续 失败的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年新建二中二模理) 函数![]() ,其中
,其中![]()
![]() 其中
其中![]() ,若
,若![]() 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于![]() .
.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)在![]() 中,
中,![]() 分别是角
分别是角![]() 的对边,
的对边,![]() ,
,![]() .当
.当![]() 最大时,
最大时,![]() , 求
, 求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com