
分析 (1)先判断出函数f(x)的对称轴是x=-$\frac{a}{2}$=1,从而求出a的值即可;(2)将a=-1代入f(x)的表达式,从而求出关于满足条件的x的不等式组,解出即可.
解答 解:(1)∵?x∈R,都有f(1+x)=f(1-x),
则函数f(x)的对称轴是x=-$\frac{a}{2}$=1,解得:a=-2;
(2)a=-1时:f(x)=x2-x+2,
若f(log2x)>f(1),
则${{(log}_{2}^{x})}^{2}$-${log}_{2}^{x}$+2>2,
解得:x>2或0<x<1,①
由log2f(x)<f(1),
得:${log}_{2}^{{x}^{2}-x+2}$<2,
即:0<x2-x+2<4,解得:1<x<2,②,
由①②得:不存在满足条件的实数x.
点评 本题考查了二次函数的性质,考查考查对数函数的性质,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
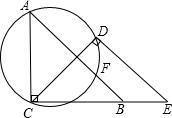 已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.
已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com