
| 生产能力分组 |  |  |  |  |  |
| 人数 | 4 | 8 |  | 5 | 3 |
| 生产能力分组 |  |  |  |  |
| 人数 | 6 | y | 36 | 18 |
 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)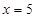 ;
;  。频率分布直方图如下:
。频率分布直方图如下: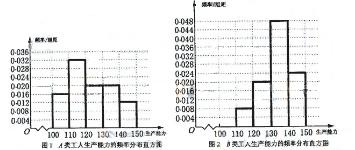
 类工人中个体间的差异程度更小。
类工人中个体间的差异程度更小。  类工人中和
类工人中和 类工人中分别抽查25名和75名。由
类工人中分别抽查25名和75名。由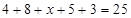 ,得
,得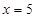 ;
; 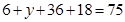 ,得
,得 。
。
 类工人中个体间的差异程度更小。
类工人中个体间的差异程度更小。 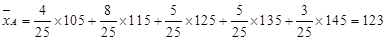
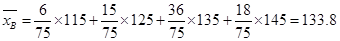 ,
,

科目:高中数学 来源:不详 题型:解答题
| 分组 | 频数 | 频率 |
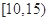 | 10 | 0.25 |
 | 26 | n |
 | m | P |
 | 1 | 0.025 |
| 合计 | M | 1 |

 的值;
的值; 内的概率.
内的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
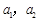 ,中位数分别为
,中位数分别为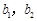 ,则有( )
,则有( )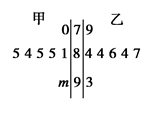
A.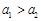 , , 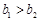 , , | B.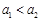 , , 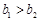 |
C.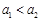 , , 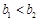 , , | D.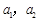 与 与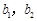 大小均不能确定 大小均不能确定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.17岁 | B.18岁 | C.17.5岁 | D.18.5岁 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.13,11,6 | B.15,11,4 | C.14,11,5 | D.16,11,3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

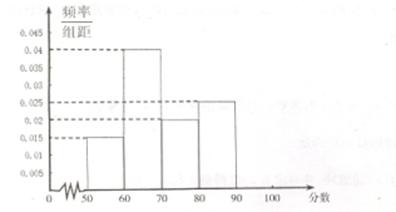
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入 (单位:百元) | 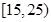 | 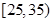 | 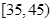 | 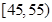 | 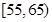 | 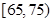 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 3 | 1 |
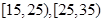 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为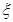 ,求随机变量
,求随机变量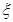 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com