
分析 (1)当$a=\frac{1}{2}$时,配方法化简f(x)=$\frac{1}{2}$x2-4x-8=$\frac{1}{2}$(x-4)2-16,从而求值域;
(2)分a=0与a≠0讨论,从而根据二次函数的性质判断函数的单调性即可.
解答 解:(1)当$a=\frac{1}{2}$时,f(x)=$\frac{1}{2}$x2-4x-8=$\frac{1}{2}$(x-4)2-16,
∵x∈[2,5],
∴-16≤$\frac{1}{2}$(x-4)2-16≤-14,
故函数f(x)在[2,5]上的值域为[-16,-14];
(2)若a=0,则f(x)=-4x-8在[2,5]上单调递减,符合题意;
若a≠0,则f(x)=a(x-$\frac{2}{a}$)2-8-$\frac{4}{a}$,其对称轴是x=$\frac{2}{a}$;
若a<0,则x=$\frac{2}{a}$<0,
所以f(x)在[2,5]上单调递减,符合题意;
若a>0,则x=$\frac{2}{a}$>0,
要使f(x)在[2,5]上是单调函数,
则$\frac{2}{a}$≤2或$\frac{2}{a}$≥5;
所以a≥1或0<a≤$\frac{2}{5}$;
综上:实数a的取值范围是:a≥1或a≤$\frac{2}{5}$.
点评 本题考查了二次函数的性质的判断与应用.


科目:高中数学 来源: 题型:选择题
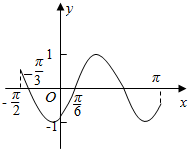 若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )
若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )| A. | $ω=2,φ=\frac{π}{3}$ | B. | $ω=2,φ=-\frac{2π}{3}$ | C. | $ω=\frac{1}{2},φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2},φ=-\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lgx2,g(x)=2lgx | B. | f(x)=1,g(x)=x0 | ||
| C. | $f(x)=\sqrt{x^2},g(x)={(\sqrt{x})^2}$ | D. | $f(x)=x,g(x)={log_a}{a^x}(a>0且a≠1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 全月应纳税所得额 | 税率(%) |
| 不超过1500元的部分 | 3 |
| 超过1500元至4500元的部分 | 10 |
| 超过4500元至9000元的部分 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{{\sqrt{2}}}{2}$.求椭圆E的方程.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{{\sqrt{2}}}{2}$.求椭圆E的方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [4,8) | C. | (4,8) | D. | (1,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com