
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.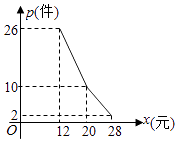
【答案】解:(I)当x∈[12,20]时,P=k1x+b1,代入点(12,26),(20,10)得k1=﹣2,b1=50,∴P=﹣2x+50;同理x∈(20,28]时,P=﹣x+30,
∴周销量P(件)与单价x(元)之间的函数关系式P= ![]() ;
;
(Ⅱ)y=P(x﹣10)﹣25= ![]() ,
,
当x∈[12,20]时,y= ![]() ,x=
,x= ![]() 时,ymax=
时,ymax= ![]() ;
;
当x∈(20,28]时,y=﹣(x﹣20)2+75,函数单调递减,∴y<75,
综上所述,x= ![]() 时,ymax=
时,ymax= ![]() .
.
【解析】(I)由图象可得当x∈[12,20]时,P=k1x+b1解得k1=﹣2,b1=50,∴P=﹣2x+50。当x∈(20,28]时,P=﹣x+30,即得周销量P(件)与单价x(元)之间的函数关系式。
(Ⅱ)由二次函数求最值得。当x∈[12,20]时,y= 2 ( x ![]() ) 2 +
) 2 +![]() ,x=
,x= ![]() 时,ymax=
时,ymax= ![]() ;当x∈(20,28]时,y=﹣(x﹣20)2+75,函数单调递减,∴y<75.
;当x∈(20,28]时,y=﹣(x﹣20)2+75,函数单调递减,∴y<75.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点. 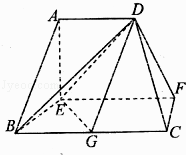
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n和为Sn , 且 ![]() 是
是 ![]() 与(an+1)2的等比中项.
与(an+1)2的等比中项.
(1)求证:数列{an}是等差数列;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 求Tn .
,数列{bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x,y的方程C:x2+y2﹣2x﹣4y+m=0
(1)当方程C表示圆时,求m的取值范围;
(2)若圆C与直线l1:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(3)在(2)条件下,若圆C上存在四点到直线l2:x﹣2y+b=0的距离均为 ![]() ,试求b的取值范围.
,试求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={x| ![]() ≤2x≤8},B={x|x>0},C={x|m<x<m+2}
≤2x≤8},B={x|x>0},C={x|m<x<m+2}
(Ⅰ)求A∩(UB);
(Ⅱ)若A∩C=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,记正方形ABCD四条边的中点为S,M,N,T,连接四个中点得小正方形SMNT.将正方形ABCD,正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1 , V2 , 则V1:V2=( ) 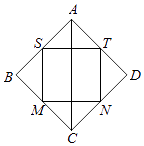
A.8:1
B.2:1
C.4:3
D.8:3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱A1B1C1﹣A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为 . 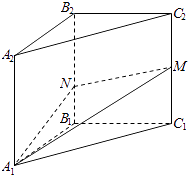
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂生产某种产品每年需要固定投资 ![]() 万元,此外每生产
万元,此外每生产 ![]() 件该产品还需要增加投资
件该产品还需要增加投资 ![]() 万元,年产量为
万元,年产量为 ![]() 件.当
件.当 ![]() 时,年销售总收入为
时,年销售总收入为 ![]() 万元;当
万元;当 ![]() 时,年销售总收入为
时,年销售总收入为 ![]() 万元.记该工厂生产并销售这种产品所得的年利润为
万元.记该工厂生产并销售这种产品所得的年利润为 ![]() 万元。
万元。
(1)求 ![]() (万元)关于
(万元)关于 ![]() (件)的函数关系式;
(件)的函数关系式;
(2)该工厂的年产量为多少件时,所得年利润最大?并求出最大值.(年利润=年销售总收入年总投资)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x∈R|2x﹣3≥0},B={x|1<x<2},C={x∈N|1≤x<a}.
(Ⅰ)求A∪B;
(Ⅱ)若C中恰有五个元素,求整数a的值;
(Ⅲ)若A∩C=,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com