
【题目】如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为 . 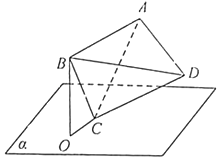
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 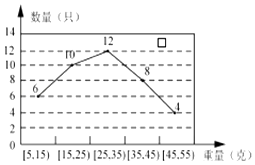
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx﹣cos2x﹣
sinxcosx﹣cos2x﹣ ![]() .
.
(Ⅰ)求函数f(x)的对称轴方程;
(Ⅱ)将函数f(x)的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移 ![]() 个单位,得到函数g(x)的图象.若a,b,c分别是△ABC三个内角A,B,C的对边,a=2,c=4,且g(B)=0,求b的值.
个单位,得到函数g(x)的图象.若a,b,c分别是△ABC三个内角A,B,C的对边,a=2,c=4,且g(B)=0,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}定义为a1>0,a11=a,an+1=an+ ![]() an2 , n∈N*
an2 , n∈N*
(1)若a1= ![]() (a>0),求
(a>0),求 ![]() +
+ ![]() +…+
+…+ ![]() 的值;
的值;
(2)当a>0时,定义数列{bn},b1=ak(k≥12),bn+1=﹣1+ ![]() ,是否存在正整数i,j(i≤j),使得bi+bj=a+
,是否存在正整数i,j(i≤j),使得bi+bj=a+ ![]() a2+
a2+ ![]() ﹣1.如果存在,求出一组(i,j),如果不存在,说明理由.
﹣1.如果存在,求出一组(i,j),如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}中,a1 , a3 , a7成等比数列,且a2n=2an﹣1,等比数列{bn}满足bn+bn+1= ![]() .
.
(1)求数列{an},{bn}的通项公式;
(2)令cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 设方程f(x)=2﹣x+b(b∈R)的四个实根从小到大依次为x1 , x2 , x3 , x4 , 对于满足条件的任意一组实根,下列判断中一定成立的是( )
设方程f(x)=2﹣x+b(b∈R)的四个实根从小到大依次为x1 , x2 , x3 , x4 , 对于满足条件的任意一组实根,下列判断中一定成立的是( )
A.x1+x2=2
B.e2<x3x4<(2e﹣1)2
C.0<(2e﹣x3)(2e﹣x4)<1
D.1<x1x2<e2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l的普通方程为x﹣y﹣2=0,曲线C的参数方程为 ![]() (θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
(θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com