
【题目】某小型餐馆一天中要购买![]() ,
,![]() 两种蔬菜,
两种蔬菜,![]() ,
,![]() 蔬菜每公斤的单价分别为2元和3元.根据需要
蔬菜每公斤的单价分别为2元和3元.根据需要![]() 蔬菜至少要买6公斤,
蔬菜至少要买6公斤,![]() 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,![]() ,
,![]() 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,计算数列
,计算数列![]() 的第100项.
的第100项.
现已给出该问题算法的流程图(如图1所示)
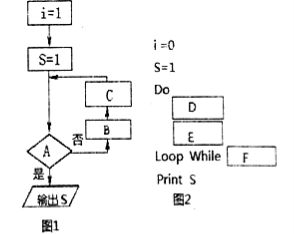
(1)请在图1中判断框的![]() (其中
(其中![]() 中用
中用![]() 的关系表示)处填上合适的语句,使之完成该问题的算法功能.
的关系表示)处填上合适的语句,使之完成该问题的算法功能.
(2)根据流程图1补充完整程序语言(如图2)(即在![]() 处填写合适的语句).
处填写合适的语句).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车![]() 店新进
店新进![]() 三类轿车,每类轿车的数量如下表:
三类轿车,每类轿车的数量如下表:
类别 |
|
|
|
数量 | 4 | 3 | 2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(1)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(2)若一次性提取4辆车,其中![]() 三种型号的车辆数分别记为
三种型号的车辆数分别记为![]() ,记
,记![]() 为
为![]() 的最大值,求
的最大值,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为解决困难职工的住房问题,决定分批建设保障性住房供给困难职工,首批计划用100万元购买一块土地,该土地可以建造每层1000平方米的楼房一幢,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元,已知建筑第1层楼房时,每平方米的建筑费用为920元.为了使该幢楼房每平方米的平均费用最低(费用包括建筑费用和购地费用),应把楼房建成几层?此时平均费用为每平方米多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α⊥平面β,α∩β=n,直线lα,直线mβ,则下列说法正确的个数是( )
①若l⊥n,l⊥m,则l⊥β;②若l∥n,则l∥β;③若m⊥n,l⊥m,则m⊥α.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga![]() (a>0,且a≠1)
(a>0,且a≠1)
(1)判断f(x)的奇偶性并证明;
(2)若对于x∈[2,4],恒有f(x)>loga![]() 成立,求m的取值范围.
成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() ,若
,若![]() ,
,![]() 均是定义在实数集R上的函数,定义函数
均是定义在实数集R上的函数,定义函数![]() =
=![]() ,则下列命题正确的是( )
,则下列命题正确的是( )
A.若![]() ,
,![]() 都是单调函数,则
都是单调函数,则![]() 也是单调函数
也是单调函数
B.若![]() ,
,![]() 都是奇函数,则
都是奇函数,则![]() 也是奇函数
也是奇函数
C.若![]() ,
,![]() 都是偶函数,则
都是偶函数,则![]() 也是偶函数
也是偶函数
D.若![]() 是奇函数,
是奇函数,![]() 是偶函数,则
是偶函数,则![]() 既不是奇函数,也不是偶函数
既不是奇函数,也不是偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
(3)若函数![]() 在区间
在区间![]() 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com