
分析 (1)f(x)为奇函数,可得f(-1)=-f(1),结合f(1)=$\frac{1}{2}$,即可求a,b的值;
(2)$f(x)=\frac{x}{{{x^2}+1}}$在(-1,1)上单调递增,用定义加以证明.
解答 解:(1)∵f(x)为奇函数,∴f(-1)=-f(1),
∴$-\frac{a}{2}+b=-(\frac{a}{2}+b)$,∴b=0,
又∵$f(1)=\frac{1}{2}$,∴$\frac{a}{2}=\frac{1}{2}$,∴a=1,
∴a=1,b=0.
(2)$f(x)=\frac{x}{{{x^2}+1}}$在(-1,1)上单调递增,
证明:设-1<x1<x2<1,
则$f({x_1})-f({x_2})=\frac{x_1}{x_1^2+1}-\frac{x_2}{x_2^2+1}$=$\frac{{{x_1}(x_2^2+1)-{x_2}(x_1^2+1)}}{(x_1^2+1)(x_2^2+1)}$=$\frac{{({x_2}-{x_1})({x_1}{x_2}-1)}}{(x_1^2+1)(x_2^2+1)}$
∵-1<x1<x2<1,
∴$(x_1^2+1)(x_2^2+1)>0$,x2-x1>0,x1x2-1<0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),
∴f(x)在(-1,1)上单调递增.
点评 本题考查了函数的性质的判断与证明及应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(a)}{a}$>$\frac{f(b)}{b}$>$\frac{f(c)}{c}$ | B. | $\frac{f(c)}{c}$>$\frac{f(b)}{b}$>$\frac{f(a)}{a}$ | C. | $\frac{f(b)}{b}$>$\frac{f(a)}{a}$>$\frac{f(c)}{c}$ | D. | $\frac{f(a)}{a}$>$\frac{f(c)}{c}$>$\frac{f(b)}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
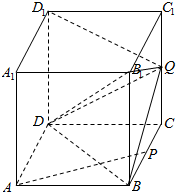 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
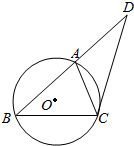 如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC的长为( )
如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC的长为( )| A. | 5 | B. | 4 | C. | $\frac{10}{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com