已知a>1,函数f(x)=loga(x2-ax+2)在x∈[2,+∞)时的值恒为正.
(1)a的取值范围;
(2)记(1)中a的取值范围为集合A,函数g(x)=log2(tx2+2x-2)的定义域为集合B.若A∩B≠∅,求实数t的取值范围.
分析:(1)欲使x
2-ax+2>1在x∈[2,+∞)时恒成立,转化成
a<x+在x∈[2,+∞)时恒成立,根据
函数
x+在[2,+∞)上的单调性求出最小值即可,使a小于最小值即可,注意条件a>1;
(2)先求出集合A,表示出集合B,根据A∩B≠∅,得不等式tx
2+2x-2>0有属于A的解,即
t>-有属于A的解,根据二次函数的性质求出
-的值域,即可求出t的范围.
解答:解:(1)x
2-ax+2>1在x∈[2,+∞)时恒成立.即
a<x+在x∈[2,+∞)时恒成立.
又函数
x+在[2,+∞)上是增函数,
所以
(x+)min=,
从而
1<a<.(6分)
(2)A=
(1,),B={x|tx
2+2x-2>0}.
由于A∩B≠∅,
所以不等式tx
2+2x-2>0有属于A的解,
即
t>-有属于A的解.(8分)
又
1<x<时,
<<1,
所以
-=
2(-)2-∈
[-,0).
故
t>-.(12分)
点评:本题主要考查了二次函数恒成立问题,以及函数的单调性等有关基础知识,同时考查了分析问题解决问题的能力,属于中档题.



 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案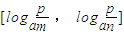 ,求实数p的取值范围;
,求实数p的取值范围;