
【题目】已知数列{an}满足 ![]() ,an+1bn=bn+1an+bn , 且
,an+1bn=bn+1an+bn , 且 ![]() (n∈N*),则数列{an}的前2n项和S2n取最大值时,n= .
(n∈N*),则数列{an}的前2n项和S2n取最大值时,n= .
【答案】8
【解析】解:由 ![]() (n∈N*),则bn=
(n∈N*),则bn= ![]() , 由an+1bn=bn+1an+bn , 当n=2k﹣1(k∈N*)为奇数时,﹣2a2k=3a2k﹣1﹣2,
, 由an+1bn=bn+1an+bn , 当n=2k﹣1(k∈N*)为奇数时,﹣2a2k=3a2k﹣1﹣2,
当n=2k(k∈N*)为偶数时,3a2k+1=﹣2a2k+3,
∴3a2k+1=3a2k﹣1+1,
∴a2k+1﹣a2k﹣1= ![]() .因此数列{a2k﹣1}成等差数列,公差为
.因此数列{a2k﹣1}成等差数列,公差为 ![]() ,首项为﹣
,首项为﹣ ![]() .
.
∴ ![]() a2k﹣1=
a2k﹣1= ![]() +
+ ![]() =
= ![]() ﹣
﹣ ![]() .
.
同理可得:a2k+2﹣a2k=﹣ ![]() .因此数列{a2k}成等差数列,公差为﹣
.因此数列{a2k}成等差数列,公差为﹣ ![]() ,首项为
,首项为 ![]() .
.
∴ ![]() =
= ![]() ×n﹣
×n﹣ ![]() ×
× ![]() =
= ![]() +2n.
+2n.
∴S2n= ![]() ﹣
﹣ ![]() +2n=﹣
+2n=﹣ ![]() +
+ ![]() n=﹣
n=﹣ ![]() (n﹣8)2+
(n﹣8)2+ ![]() .
.
∴当n=8时,数列{an}的前2n项和S2n取最大值 ![]() 时.
时.
所以答案是:8.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 对于线性回归方程![]() ,直线必经过点
,直线必经过点![]()
B. 茎叶图的优点在于它可以保存原始数据,并且可以随时记录
C. 将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变
D. 掷一枚均匀硬币出现正面向上的概率是![]() ,那么一枚硬币投掷2次一定出现正面
,那么一枚硬币投掷2次一定出现正面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

现对某城市30天的空气质量进行监测,获得30个API数据(每个数据均不同),统计绘得频率分布直方图如图.
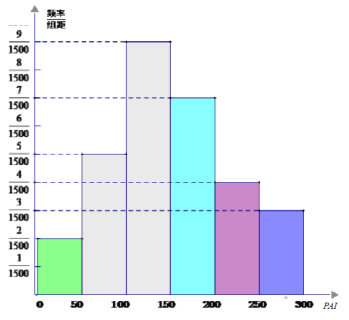
(1)请由频率分布直方图来估计这30天API 的平均值;
(2)若从获得的“空气质量优”和“空气质量中重度污染” 的数据中随机选取![]() 个数据进行复查,求“空气质量优”和“空气质量中重度污染”数据恰均被选中的概率;
个数据进行复查,求“空气质量优”和“空气质量中重度污染”数据恰均被选中的概率;
(3)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API (记为![]() )的关系式为
)的关系式为 ,
,
若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不超过600元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536~1611),是中国明代一位杰出的音乐家、数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度13个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为![]() ,第七个音的频率为
,第七个音的频率为![]() ,则
,则![]() =
=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.

(1) 求直线PB与平面POC所成角的余弦值;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com