
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:
分成6组,制成频率分布直方图如下:
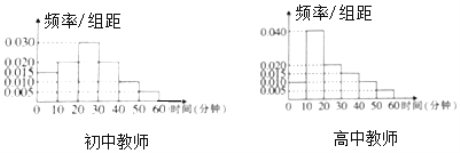
假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
(1)试估计本校教师中缺乏锻炼的人数;
(2)若从参与调查,且每天课外锻炼时间在![]() 内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
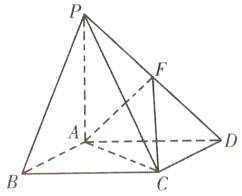
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场推出消费抽现金活动,顾客消费满1000元可以参与一次抽奖,该活动设置了一等奖、二等奖、三等奖以及参与奖,奖金分别为:一等奖200元、二等奖100元、三等奖50元、参与奖20元,具体获奖人数比例分配如图,则下列说法中错误的是( )

A.获得参与奖的人数最多
B.各个奖项中一等奖的总金额最高
C.二等奖获奖人数是一等奖获奖人数的两倍
D.奖金平均数为![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E,F分别是棱
,E,F分别是棱![]() ,
,![]() 的中点.
的中点.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与底面ABC所成的角的大小.
与底面ABC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学一班级1999级同学举行20周年聚会,该班共来了12位同学,其中女同学6位,聚会过程中有一个游戏环节,在游戏环节中,需要随机从中选出2位同学代表,进行男女搭配完成该项游戏,因此,每次选出的2位同学是一男一女,才算“有效选择”;否则视为“无效选择”,继续下一次选择,直到成为“有效选择”为止.
(1)求第一次随机选出的2位同学是“有效选择”的概率;
(2)设第一次选出的2位同学代表中女同学人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为![]() (θ为参数).
(θ为参数).
(1)当![]() 时,求直线l与曲线C的普通方程;
时,求直线l与曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,直线l倾斜角的范围为(0,![]() ],且P点的直角坐标为(0,2),求
],且P点的直角坐标为(0,2),求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com