练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

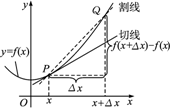
    如图所示：设曲线C上一点P(x，f(x))，过点P的一条割线交曲线C于另一点Q(x＋Δx，f(x＋Δx))，则割线PQ的斜率为KPQ＝_________＝_________．当点Q沿曲线C向点P运动，并无限趋近于点P时，即Δx→0时，割线PQ逼近点P的切线V．从而割线的斜率逼近_________，无限趋近于P(x，f(x))处的切线的_________．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

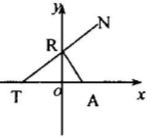    精英家教网如图所示，点A（1，0）．点R在y轴上运动，T在x轴上，N为动点，且
    RT
    •
    RA
    =0，
    RN
    +
    RT
    =0，
    （1）设动点N的轨迹为曲线C，求曲线C的方程；
    （2）过点B（-2，0）的直线l与曲线C交于点P、Q，若在曲线C上存在点M，使得△MPQ为以PQ为斜边的直角三角形，求直线l的斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图所示，在直角坐标系xOy中，射线OA在第一象限，且与x轴的正半轴成定角60°，动点P在射线OA上运动，动点Q在y轴的正半轴上运动，△POQ的面积为2
    		3
    ．
    （1）求线段PQ中点M的轨迹C的方程；
    （2）R1，R2是曲线C上的动点，R1，R2到y轴的距离之和为1，设u为R1，R2到x轴的距离之积．问：是否存在最大的常数m，使u≥m恒成立？若存在，求出这个m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，在Rt△ABC中，∠CAB=90°，AB=2，AC=
    		2
    2
    ．一曲线E过点C，动点P在曲线E上运动，且保持|PA|+|PB|的值不变，直线l经过A与曲线E交于M，N两点．
    （1）建立适当的直角坐标系，求曲线E的方程；
    （2）设直线l的斜率为k，若∠MBN为钝角，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
    （A）（极坐标与参数方程）直线l：x-y+b=0与曲线
    x=1+
    		2
    cosθ
    y=-2+
    		2
    sinθ
    (θ    是参数）相切，则b=
    -1或-5
    -1或-5
    ．
    （B）设6≤|x-a|+|x-b|对任意的x∈R恒成立．则a与b满足的关系是
    |a-b|≥6
    |a-b|≥6
    ．
    （C）如图所示，圆O的直径为6，C为圆周上一点．BC=3，过C作圆的切线l．过A作l的垂线AD，垂足为D，则线段CD的长为
    3
    		3
    2
    3
    		3
    2
    ．

    查看答案和解析>>

    同步练习册答案