
分析 (1)根据题意,设x<0,则-x>0,结合函数在x≥0时的解析式,可得x<0的解析式,综合可得答案;
(2)由函数的解析式,分2种情况进行计算,分别求出a的值,综合可得答案.
解答 解:(1)设x<0,则-x>0,
∴f(-x)=-2x+3,
又f(x)为偶函数,∴f(-x)=f(x),
∴f(x)=-2x+3(x<0),
故$f(x)=\left\{\begin{array}{l}2x+3,x≥0\\-2x+3,x<0\end{array}\right.$.
(2)当a≥0时,f(a)=2a+3=7⇒a=2;
当a<0时,f(a)=-2a+3=7⇒a=-2.
故a=±2.
点评 本题考查函数的奇偶性与单调性的综合应用,关键是充分利用函数的奇偶性求出函数的解析式.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
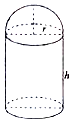 某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.
某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
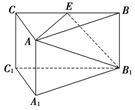 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AE与B1C1是异面直线,且AE⊥B1C1 | ||
| C. | AC⊥平面ABB1A1 | D. | A1C1∥平面AB1E |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com