
����Ŀ������1����2��������״��������ķ��ײ�����Ȼ���࣬Ϊ���Ͽ����鴫���������ص���Ⱥ��Ԥ��������ij������ͳ�Ʒ�����Ա![]() �ˣ�����
�ˣ�����![]() �꼰���ϵĹ���
�꼰���ϵĹ���![]() ��.��
��.��![]() ����ȷ�����
����ȷ�����![]() ��������
��������![]() �����µ���ռ
�����µ���ռ![]() .
.
��1���뽫������������������������ж��Ƿ���![]() %�İ�����Ϊ�Ƿ�ȷ�ﻼ�¹ڷ����������йأ�
%�İ�����Ϊ�Ƿ�ȷ�ﻼ�¹ڷ����������йأ�
ȷ�ﻼ�¹ڷ��� | δȷ�ﻼ�¹ڷ��� | �ϼ� | |
50�꼰���� | 40 | ||
50������ | |||
�ϼ� | 10 | 100 |
��2��Ϊ���о�����״�����Ĵ�ȾԴ�ʹ�����ʽ����![]() ��ȷ����Ա��������
��ȷ����Ա��������![]() �˼�������Ѫ����о���
�˼�������Ѫ����о���![]() ��ʾ����ȡ��
��ʾ����ȡ��![]() ����
����![]() �����µ���������
�����µ���������![]() �ķֲ����Լ���ѧ����.
�ķֲ����Լ���ѧ����.
�����
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
�ο���ʽ��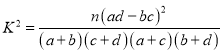 ������
������![]() .
.
���𰸡���1���������������![]() %�İ�����Ϊ�Ƿ�ȷ�ﻼ�¹ڷ����������йأ�2���������
%�İ�����Ϊ�Ƿ�ȷ�ﻼ�¹ڷ����������йأ�2���������
��������
(1)�����ⲹ��![]() ���������ٴ���
���������ٴ��� �����
�����![]() �����жϣ�
�����жϣ�
(2)����������ȷ��![]() ��ֵ����Ϊ
��ֵ����Ϊ![]() ��Ȼ��ֱ�������ǵĶ�Ӧ�ĸ��ʣ���������ĸ����г��ֲ����Լ��������ֵ.
��Ȼ��ֱ�������ǵĶ�Ӧ�ĸ��ʣ���������ĸ����г��ֲ����Լ��������ֵ.
�⣺��1���������������£�
ȷ�ﻼ�¹ڷ��� | δȷ�ﻼ�¹ڷ��� | �ϼ� | |
50������ | 7 | 33 | 40 |
50������ | 3 | 57 | 60 |
�ϼ� | 10 | 90 | 100 |
![]() .
.
������![]() %�İ�����Ϊ�Ƿ�ȷ�ﻼ�¹ڷ����������й�.
%�İ�����Ϊ�Ƿ�ȷ�ﻼ�¹ڷ����������й�.
��2���������⣬![]() ��ֵ����Ϊ
��ֵ����Ϊ![]() .
.
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]() ��.
��.


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex��x+1��2����f1��x��=f'��x����fn+1��x��=fn'��x������fn��x��=ex��anx2+bnx+cn����������{![]() }��ǰn���ΪSn��������ѡ������S2019��ֵ��ӽ�����( )
}��ǰn���ΪSn��������ѡ������S2019��ֵ��ӽ�����( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˫����E��![]() ��
��![]() ��
��![]() �������ҽ���ֱ�Ϊ
�������ҽ���ֱ�Ϊ![]() ��
��![]() ����֪��
����֪��![]() Ϊ������C��
Ϊ������C��![]() �Ľ��㣬�ҵ�˫����E��һ�������ߵľ���Ϊ
�Ľ��㣬�ҵ�˫����E��һ�������ߵľ���Ϊ![]() ���ֵ�PΪ˫����E��һ�㣬����
���ֵ�PΪ˫����E��һ�㣬����![]() .��
.��
��1��˫���ߵı�����Ϊ______��
��2��![]() ������Բ�뾶�����Բ�뾶֮��Ϊ______.
������Բ�뾶�����Բ�뾶֮��Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���![]() �У�E��F��
��E��F��![]() ��
��![]() �е㣬
�е㣬![]() ��
��![]() ��
��![]() ����
����![]() �ضԽ���
�ضԽ���![]() ������
������![]() ��ʹƽ��
��ʹƽ��![]() ƽ��
ƽ��![]() ����������
����������![]() �У����н��۲���ȷ���ǣ� ��
�У����н��۲���ȷ���ǣ� ��
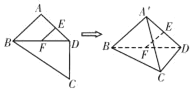
A.![]() ƽ��
ƽ��![]() B.����ֱ��
B.����ֱ��![]() ��
��![]() ���ɵĽ�Ϊ90��
���ɵĽ�Ϊ90��
C.����ֱ��![]() ��
��![]() ���ɵĽ�Ϊ60��D.ֱ��
���ɵĽ�Ϊ60��D.ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ30��
���ɵĽ�Ϊ30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���֪��Բ
�У���֪��Բ![]() ��������
��������![]() ����Ϊ
����Ϊ![]() ������A��б��Ϊ
������A��б��Ϊ![]() ��ֱ��l����ԲC�ڵ�D����y���ڵ�E.
��ֱ��l����ԲC�ڵ�D����y���ڵ�E.
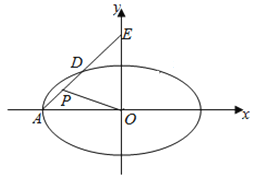
��1������ԲC�ķ��̣�
��2����֪��PΪ![]() ���е㣬�Ƿ���ڶ���Q�����������
���е㣬�Ƿ���ڶ���Q�����������![]() ����
����![]() �������ڣ������Q�����꣬�������ڣ�˵�����ɣ�
�������ڣ������Q�����꣬�������ڣ�˵�����ɣ�
��3��������O��ֱ��l��ƽ���߽���ԲC�ڵ�M����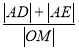 ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�ĵ���ABCD�������Σ�PA�͵���ABCD��E��F�ֱ���AC��PB���е㣮
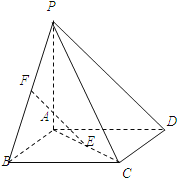
��1��֤����EF��ƽ��PCD��
��2����֤����PBD����PAC��
��3����PA=AB����PD��ƽ��PAC���ɽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
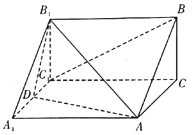
����Ŀ����ͼ����������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
Ϊ��![]() �ϵĶ���.
�ϵĶ���.
��1����![]() Ϊ
Ϊ![]() ���е㣬��֤��
���е㣬��֤��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ƽ��ABC����
ƽ��ABC����![]() �Ƿ���ڵ�
�Ƿ���ڵ�![]() ��ʹ�����
��ʹ�����![]() ��ƽ��ǵ�����ֵΪ
��ƽ��ǵ�����ֵΪ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4-4�����������������]
��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() �Dz�������������ԭ��
�Dz�������������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��������![]() �ļ����귽�̺�����
�ļ����귽�̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2��������![]()
![]() ������
������![]() ����
����![]() ��
��![]() ���㣬������
���㣬������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ȡ���ֵʱ
ȡ���ֵʱ![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
�У�![]() ƽ��
ƽ��![]() ���ı���
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�![]() ��
��![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() ��
��![]() ���е�.
���е�.
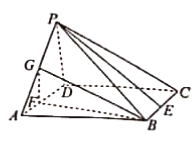
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() �����
�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com