
【题目】如图,在正三棱柱![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点,且
上的动点,且![]() .
.
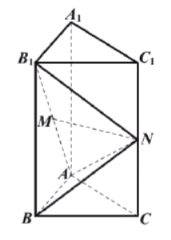
(1)若![]() ,求证:
,求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,求
,求![]() 的最大值
的最大值
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:
【题目】在杨辉三角形中,从第2行开始,除1以外,其它每一个数值是它上面的两个数值之和,该三角形数阵开头几行如图所示.

(1)在杨辉三角形中是否存在某一行,使该行中三个相邻的数之比是3∶4∶5?若存在,试求出是第几行;若不存在,请说明理由;
(2)已知n,r为正整数,且n≥r+3.求证:任何四个相邻的组合数C,C![]() ,C
,C![]() ,C
,C![]() 不能构成等差数列.
不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:
(单位:![]() ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量![]() (单位:
(单位:![]() ) 和时段投入成本
) 和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
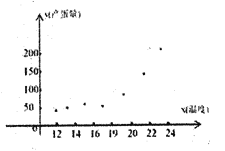
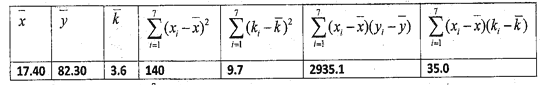
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为
,当时段控制温度为![]() 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为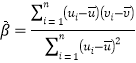 ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0),且圆C:x2+y2﹣6x+4y+4=0.
(Ⅰ)当直线![]() 过点P且与圆心C的距离为1时,求直线
过点P且与圆心C的距离为1时,求直线![]() 的方程;
的方程;
(Ⅱ)设过点P的直线与圆C交于A、B两点,若|AB|=4,求以线段AB为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】合肥一中、六中为了加强交流,增进友谊,两校准备举行一场足球赛,由合肥一中版画社的同学设计一幅矩形宣传画,要求画面面积为![]() ,画面的上、下各留
,画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.

(1)如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
(2)设画面的高与宽的比为![]() ,且
,且![]() ,求
,求![]() 为何值时,宣传画所用纸张面积最小?
为何值时,宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对昼夜温差大小与某种子发芽多少之间的关系进行研究,下面是3月1日至5日每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数的详细记录:
(1)根据3月2日至3月4日的数据,用最小二乘法求出y关于x的线性回归方程;
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均小于2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
参考公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com