
[番茄花园1] 如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
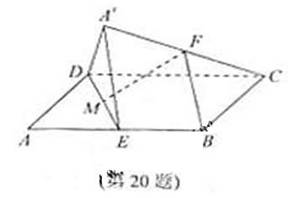 (Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
[番茄花园1]1.
[番茄花园1] 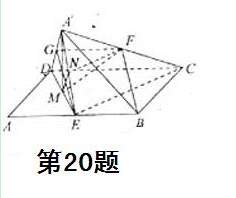 .解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
.解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=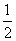 CD.
CD.
BE∥CD,BE=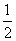 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,
所以BF∥EG
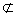 因为
因为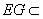 平面
平面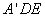 ,BF
,BF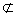 平面
平面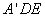
所以 BF//平面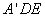
(Ⅱ)解:在平行四边形,ABCD中,设BC=a
则AB=CD=2a, AD=AE=EB=a,
连CE
因为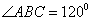
在△BCE中,可得CE=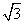 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=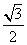 a,
MN=
a,
MN=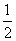 a,
FM=a,
a,
FM=a,
则cos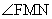 =
=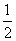 .
.
所以直线FM与平面A′DE所成角的余弦值为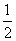 .
.
证明:存在实数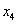 ,使得
,使得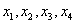 按某种顺序排列后的等差数列,并求
按某种顺序排列后的等差数列,并求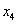
[番茄花园1]20.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com