
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= ![]() AB=1,M为PB中点.
AB=1,M为PB中点. 
(1)证明:CM∥平面PAD;
(2)求二面角A﹣MC﹣B的余弦值.
【答案】
(1)证明:取AB中点N,连结MN,CN,
∵四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,
∠DAB=90°,
PA⊥底面ABCD,且PA=AD=DC= ![]() AB=1,
AB=1,
M为PB中点,
∴MN∥PA,CN∥AD,
∵MN∩CN=N,PA∩AD=A,MN,
CN平面MNC,PA,AD平面PAD,
∴平面MNC∥平面PAD,
∵CM平面MNC,∴CM∥平面PAD.
(2)解:以A为原点,AD,AB,AP为x,y,z轴,建立空间直角坐标系,
A(0,0,0),C(1,1,0),P(0,0,1),B(0,2,0),M(0,1, ![]() ),
),
![]() =(1,0,﹣
=(1,0,﹣ ![]() ),
), ![]() =(0,﹣1,﹣
=(0,﹣1,﹣ ![]() ),
), ![]() =(0,1,﹣
=(0,1,﹣ ![]() ),
),
设平面AMC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 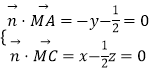 ,取z=2,得
,取z=2,得 ![]() =(1,﹣1,2),
=(1,﹣1,2),
设平面BMC的法向量 ![]() =(a,b,c),
=(a,b,c),
则 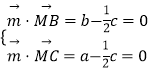 ,取c=2,得
,取c=2,得 ![]() =(1,1,2),
=(1,1,2),
设二面角A﹣MC﹣B的平面角为θ,
则cosθ=﹣ ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴二面角A﹣MC﹣B的余弦值为﹣ ![]() .
.
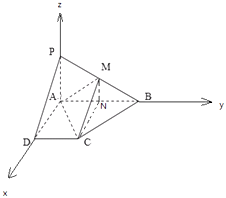
【解析】(1)取AB中点N,连结MN,CN,推导出平面MNC∥平面PAD,由此能证明CM∥平面PAD.(2)以A为原点,AD,AB,AP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣MC﹣B的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两解的是( )
A.a=7,b=14,A=30°
B.b=4,c=5,B=30°
C.b=25,c=3,C=150°
D.a= ![]() ,b=
,b= ![]() ,B=60°
,B=60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分),设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°。 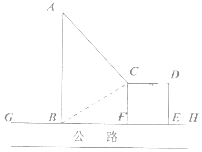
(1)求y关于x的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:x取何值时,该公司建设中转站围墙和两条道路总造价M最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1)(n∈N*)
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:an= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令cn= ![]() (n∈N*),求数列{cn}的前n项和Tn .
(n∈N*),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以 ![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为 ![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):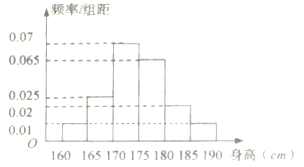
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在 ![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在 ![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. (I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.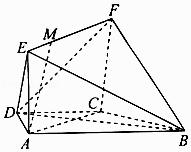
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com