
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米, ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 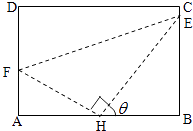
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若 ![]() ,求此时管道的长度L;
,求此时管道的长度L;
(3)当θ取何值时,污水净化效果最好?并求出此时管道的长度.
【答案】
(1)解: ![]() ,
, ![]() ,
,
![]() .
.
由于 ![]() ,
, ![]() ,
,
所以 ![]() ,
,
所以 ![]() .
.
所以 ![]() ,
, ![]()
(2)解:当 ![]() 时,
时,
![]() ,
,
![]() (米)
(米)
(3)解: ![]() ,
,
设sinθ+cosθ=t,
则 ![]() ,
,
所以 ![]() .
.
由于 ![]() ,
,
所以 ![]() .
.
由于 ![]() 在
在 ![]() 上单调递减,
上单调递减,
所以当 ![]() 即
即 ![]() 或
或 ![]() 时,
时,
L取得最大值 ![]() 米.
米.
答:当 ![]() 或
或 ![]() 时,污水净化效果最好,此时管道的长度为
时,污水净化效果最好,此时管道的长度为 ![]() 米
米
【解析】(1)由∠BHE=θ,H是AB的中点,易得 ![]() ,
, ![]() ,
, ![]() ,由污水净化管道的长度L=EH+FH+EF,则易将污水净化管道的长度L表示为θ的函数.(2)若
,由污水净化管道的长度L=EH+FH+EF,则易将污水净化管道的长度L表示为θ的函数.(2)若 ![]() ,结合(1)中所得的函数解析式,代入易得管道的长度L的值.(3)污水净化效果最好,即为管道的长度最长,由(1)中所得的函数解析式,结合三角函数的性质,易得结论.
,结合(1)中所得的函数解析式,代入易得管道的长度L的值.(3)污水净化效果最好,即为管道的长度最长,由(1)中所得的函数解析式,结合三角函数的性质,易得结论.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】有以下命题:
①如果向量 ![]() ,
, ![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么 ![]() ,
, ![]() 的关系是不共线;
的关系是不共线;
②O,A,B,C为空间四点,且向量 ![]() ,
, ![]() ,
, ![]() 不构成空间的一个基底,则点O,A,B,C一定共面;
不构成空间的一个基底,则点O,A,B,C一定共面;
③已知向量 ![]() ,
, ![]() ,
, ![]() 是空间的一个基底,则向量
是空间的一个基底,则向量 ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() 也是空间的一个基底;
也是空间的一个基底;
④△ABC中,A>B的充要条件是sinA>sinB.
其中正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() ),其图象相邻两条对称轴之间的距离为
),其图象相邻两条对称轴之间的距离为 ![]() ,且函数f(x+
,且函数f(x+ ![]() )是偶函数,下列判断正确的是( )
)是偶函数,下列判断正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点( ![]() ,0)d对称
,0)d对称
C.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
D.函数f(x)在[ ![]() ,π]上单调递增
,π]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,已知an>0,a1+a2+a3=15,且a1+2,a2+5,a3+13构成等比数列{bn}的前三项.
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示.

(1)求100名使用者中各年龄组的人数,并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2)若已从年龄在![]() 的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角α﹣AB﹣β是直二面角,P为棱AB上一点,PQ、PR分别在平面α、β内,且∠QPB=∠RPB=45°,则∠QPR为( )
A.45°
B.60°
C.120°
D.150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com