
【题目】已知点A(1,0),圆E:(x+1)2+y2=16,点B是圆E上任意一点,线段AB的垂直平分线l与半径EB相交于H.
(1)当点B在圆上运动时,求动点H的轨迹г的方程:
(2)过点A且与坐标轴不垂直的直线交轨迹г于![]() 、
、![]() 两点,线段OA(O为坐标原点)上是否存在点
两点,线段OA(O为坐标原点)上是否存在点![]() 使得
使得![]() 若存在,求出实数m的取值范围;若不存在,说明理由.
若存在,求出实数m的取值范围;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
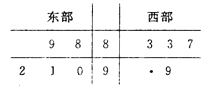
其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了![]() 位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示)
位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示)
年龄x(岁) |
|
|
|
|
周均学习成语知识时间y(小时) |
|
|
|
|
由表中数据,试求线性回归方程![]() ,并预测年龄为
,并预测年龄为![]() 岁观众周均学习成语知识时间.
岁观众周均学习成语知识时间.
参考公式: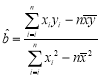 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,O为坐标原点,以O为圆心的圆与直线
中,O为坐标原点,以O为圆心的圆与直线![]() 相切.
相切.
(1)求圆O的方程.
(2)直线![]() 与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形
与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形![]() 为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是圆O:x2+y2=16上的任意一点,l是过点A且与x轴垂直的直线,B是直线l与x轴的交点,点Q在直线l上,且满足4|BQ|=3|BA|.当点A在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)已知直线y=kx﹣2(k≠0)与曲线C交于M,N两点,点M关于y轴的对称点为M′,设P(0,﹣2),证明:直线M′N过定点,并求△PM′N面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 前
前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,
,![]() 为
为![]() 的前
的前![]() 项和,求证:
项和,求证:![]() .
.
(3)在(2)的条件下,若数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,求证
,求证![]()
(4)请你说明第(3)问所用到的求和方法,哪些数列通项的模型适合此方法?请举例说明.(至少列举出三种)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,它与曲线
,它与曲线![]() 的交点为
的交点为![]() ,
,![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com