【答案】
分析:(1)由已知,可求出a
n=n,从而不等式化为

,整理为

,得出m=2,n=1
(2)先用数学归纳法证明b
n>n+2,由此b
k+1=b
k2-k•b
k+1=b
k(b
k-k)+1>2b
k+1,两边同时加上1,并整理得1+b
k+1>2(1+b
k ),得出1+b
n>2(1+b
n-1)>2
2(1-b
n-2)>…>2
n-1(1+b
1)=5•2
n-1,得出
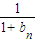 <
< ×(
×( )n-1
)n-1,对不等式的右边各项放缩,再结合等比数列求和公式,计算化简,可以证明.
解答:解:(1)由题意,∵a
22=a
1•a
4,
∴(1+d)
2=1+3d,∴d=1
∴a
n=n,

∴

∵

∴
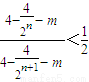
∴

∴m=2,n=1;
(2)先用数学归纳法证明b
n>n+2
当n=1时,b
1=4>1+2,不等式成立.
假设n=k(k∈N,k≥1)时,不等式成立,即b
k>k+2.则当n=k+1时,b
k+1=b
k2-k•b
k+1=b
k(b
k-k)+1>(k+2)×2+1=2k+5>(k+1)+2,即当n=k+1时,不等式也成立.
所以对于任意正整数n均有b
n>n+2
由此b
k+1=b
k2-k•b
k+1=b
k(b
k-k)+1>2b
k+1,两边同时加上1,并整理得1+b
k+1>2(1+b
k ),∴1+b
n>2(1+b
n-1)>2
2(1-b
n-2)>…>2
n-1(1+b
1)=5•2
n-1,
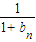 <
< ×(
×( )n-1
)n-1,
∴
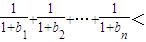
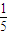
(1+

+

+

)=
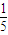
×

=
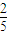
[1-

]<
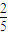
.
点评:本题考查等差数列、等比数列通项公式,前n项和公式,放缩法证明不等式,考查分析、构造、转化、计算能力.

 的前n项和为Sn.
的前n项和为Sn. ,求正整数m,n的值;
,求正整数m,n的值; .
. ,整理为
,整理为 ,得出m=2,n=1
,得出m=2,n=1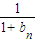 <
< ×(
×( )n-1,对不等式的右边各项放缩,再结合等比数列求和公式,计算化简,可以证明.
)n-1,对不等式的右边各项放缩,再结合等比数列求和公式,计算化简,可以证明.


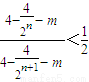

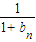 <
< ×(
×( )n-1,
)n-1,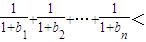
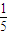 (1+
(1+ +
+ +
+ )=
)=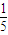 ×
× =
=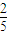 [1-
[1- ]<
]<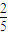 .
.
