[题目]阅读程序框图.运行相应的程序.则输出的T值为( ) A.22B.24C.39D.41 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】阅读程序框图，运行相应的程序，则输出的T值为（）
A.22
B.24
C.39
D.41

【答案】C
【解析】解：第1次执行循环体后，S=1，不满足退出循环的条件，故n=3；

第2次执行循环体后，S=32﹣1=8，不满足退出循环的条件，故n=5；

第3次执行循环体后，S=52﹣8=17，不满足退出循环的条件，故n=7；

第4次执行循环体后，S=72﹣17=32，满足退出循环的条件，

故输出的T=S+n=32+7=39，

故选：C

【考点精析】解答此题的关键在于理解程序框图的相关知识，掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知f（x）为R上的可导函数，且对x∈R，均有f（x）＞f′（x），则有（）
A.e2016f（﹣2016）＜f（0），f（2016）＜e2016f（0）
B.e2016f（﹣2016）＞f（0），f（2016）＞e2016f（0）
C.e2016f（﹣2016）＜f（0），f（2016）＞e2016f（0）
D.e2016f（﹣2016）＞f（0），f（2016）＜e2016f（0）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是边长为 3 的菱形，∠ABC=60°，PA⊥平面ABCD，PA=3，F 是棱 PA上的一个动点，E为PD的中点．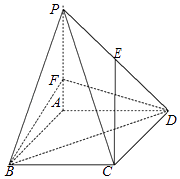
（Ⅰ）若 AF=1，求证：CE∥平面 BDF；
（Ⅱ）若 AF=2，求平面 BDF 与平面 PCD所成的锐二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知α∈[0，π），在直角坐标系xOy中，直线l1的参数方程为（t为参数）；在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l2的极坐标方程是ρcos（θ﹣α）=2sin（α+ ）．
（Ⅰ）求证：l1⊥l2
（Ⅱ）设点A的极坐标为（2，），P为直线l1 ， l2的交点，求|OP||AP|的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：

质量指标值分组	[75，85）	[85，95）	[95，105）	[105，115）	[115，125）
频数	6	26	38	22	8

（1）作出这些数据的频数分布直方图；
（2）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中间值来代表这种产品质量的指标值）；
（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的85%”的规定？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50），[50，60），…，[80，90），[90，100]．
（Ⅰ）求频率分布直方图中a的值；
（Ⅱ）估计该企业的职工对该部门评分不低于80的概率；
（Ⅲ）从评分在[40，60）的受访职工中，随机抽取2人，求此2人的评分都在[40，50）的概率．