
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() 满足
满足![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,其前7项和为42.
,其前7项和为42.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)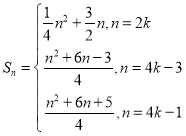 ,
,![]()
【解析】
试题分析:(1)由已知得数列![]() 是等差数列,从而易得
是等差数列,从而易得![]() 的通项公式,求得
的通项公式,求得![]() ,利用
,利用![]() 求得
求得![]() ,再求得
,再求得![]() 可得数列
可得数列![]() 通项,利用已知
通项,利用已知![]() 可得
可得![]() ,又
,又![]() 得
得![]() 是等差数列,由等差数列的基本量法可求得
是等差数列,由等差数列的基本量法可求得![]() ;(2)代入
;(2)代入![]() 得
得![]() ,变形后得
,变形后得![]() ,从而易求得和
,从而易求得和![]() ,于是有
,于是有![]() ,只要求得
,只要求得![]() 的最大值即可得
的最大值即可得![]() 的最小值,从而得
的最小值,从而得![]() 的范围,研究
的范围,研究![]() 的单调性可得;(3)根据新数列的构造方法,在求新数列的前
的单调性可得;(3)根据新数列的构造方法,在求新数列的前![]() 项和
项和![]() 时,对
时,对![]() 分类:
分类:![]() ,
,![]() 和
和![]() (
(![]() )三类,可求解.
)三类,可求解.
试题解析:(1)∵![]() ,∴数列
,∴数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,
的等差数列,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() .............................3分
.............................3分
∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,∴数列
,∴数列![]() 是等差数列,且公差为
是等差数列,且公差为![]() ,设
,设![]() 的前
的前![]() 项和为
项和为![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ...................5分
...................5分
(2)由(1)知![]() ,
,
∴![]()
![]() ,
,
∴![]() .......................7分
.......................7分
设![]() ,则
,则![]() ,
,
∴数列![]() 为递增数列,.........................9分
为递增数列,.........................9分
∴![]() ,
,
∵对任意正整数![]() ,都有
,都有![]() 恒成立,∴
恒成立,∴![]() ..........................10分
..........................10分
(3)数列![]() 的前
的前![]() 项和
项和![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,
,
①当![]() 时,
时,![]()
![]() ;
;
②当![]() 时,
时,![]() ,
,
特别地,当![]() 时,
时,![]() 也符合上式;
也符合上式;
③当![]() 时,
时,![]()
![]() .
.
综上: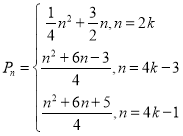 ,
,![]() ...................................16分
...................................16分


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】
某园艺公司种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了![]() 棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 2 | 4 | 11 | 16 | 13 | 4 |
(Ⅰ)在这批树苗中任取一棵,其高度在![]() 厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
(Ⅱ)为了进一步获得研究资料,标记![]() 组中的树苗为
组中的树苗为![]() ,
,![]() 组中的树苗为
组中的树苗为![]() ,现从
,现从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出的概率是多少?
同时被移出的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
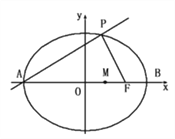
【题目】如图,A、B分别是椭圆![]() 的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
(1)点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:(x﹣1)2+(y﹣1)2=4,直线l过点P(2,3)且与圆M交于A,B两点,且|AB|=2 ![]() .
.
(1)求直线l方程;
(2)设Q(x0 , y0)为圆M上的点,求x02+y02的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 的参数方程是
的参数方程是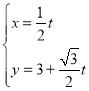 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
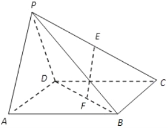
【题目】底面是正方形的四棱锥中![]() 中,侧面
中,侧面![]() 底面
底面![]() ,且
,且![]() 是等腰直角三角形,其中
是等腰直角三角形,其中![]() ,
,![]() 分别为线段
分别为线段![]() 的中点,问在线段
的中点,问在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请求出点
,若存在,请求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)关于![]() 的不等式
的不等式![]() 在
在![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,
, ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com