已知函数
（1）当
时，求函数
取得最大值和最小值时
的值；
（2）设锐角
的内角A、B、C的对应边分别是
，且
，若向量
与向量
平行，求
的值.
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝2sin
cos＋
cos
.
（1）求函数f(x)的最小正周期及最值；
（2）令g(x)＝f
，判断函数g(x)的奇偶性，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图所示，点O为做简谐运动的物体的平衡位置，取向右的方向为物体位移的正方向，若已知振幅为3 cm，周期为3 s，且物体向右运动到A点(距平衡位置最远处)开始计时．(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式；(2)求该物体在t＝5 s时的位置．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（12分）（2011•广东）已知函数f（x）=2sin（
x﹣
），x∈R．
（1）求f（0）的值；
（2）设α，β∈
，f（3
）=
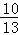，f（3β+
）=
．求sin（α+β）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(2014·大庆模拟)已知向量a=(
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
(1)求ω的值.
(2)设α,β∈
,f
=
,f
=-
,求sin(α+β)的值.
(3)若x∈[-π,π],求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时，
取得最大值；
时，
.
，由于
，
，将
看作一个整体结合正弦函数的图象可得
.由
得
，所以
得
时，
与向量
平行，所以
即
，又
.由余弦定理得
，这样根据角C的范围便得边
的范围；再据题设
，即可得
4分 
， 
即
图象的一部分如图所示．
的解析式；
时，求函数
的最大值与最小值及相应的
的值．
)(x≠0)，且cosα＝
x，求sinα、tanα的值．
在
内只取到一个最大值和一个最小值，且当
时，
；当
时，
.(1)求此函数的解析式；(2)求此函数的单调递增区间．
，
.
值； (2)求
的值.