
分析 (1)先求出其导函数,求出切线斜率,即可求曲线f(x)在x=2处的切线方程;
(2)先求出函数h(x)的导函数,分情况讨论让其大于0求出增区间,小于0求出减区间即可得到函数的单调区间;
(3)先把f(x0)<g(x0)成立转化为h(x0)<0,即函数h(x)=x+$\frac{1+a}{x}$在[1,e]上的最小值小于零;再结合(Ⅱ)的结论分情况讨论求出其最小值即可求出a的取值范围.
解答 解:(1)当a=1时,f(x)=x-lnx,f′(x)=1-$\frac{1}{x}$,
$f'(2)=\frac{2-1}{2}=\frac{1}{2}$,f(2)=2-ln2,
所以函数f(x)在(2,f(2))处的切线方程是$y-({2-ln2})=\frac{1}{2}({x-2})$,
即x-2y+2-2ln2=0;
(2)h(x)=x+$\frac{1+a}{x}$-alnx,h′(x)=1-$\frac{1+a}{{x}^{2}}$-$\frac{a}{x}$=$\frac{(x+1)(x-1-a)}{{x}^{2}}$,
①当a+1>0时,即a>-1时,在(0,1+a)上h'(x)<0,
在(1+a,+∞)上h'(x)>0,
所以h(x)在(0,1+a)上单调递减,在(1+a,+∞)上单调递增;
②当1+a≤0,即a≤-1时,在(0,+∞)上h'(x)>0,
所以,函数h(x)在(0,+∞)上单调递增.
(3)在[1,e]上存在一点x0,使得f(x0)<g(x0)成立,
即在[1,e]上存在一点x0,使得h(x0)<0,
即函数h(x)=x+$\frac{1+a}{x}$-alnx在[1,e]上的最小值小于零.
由(2)可知①即1+a≥e,即a≥e-1时,h(x)在[1,e]上单调递减,
所以h(x)的最小值为h(e),
由h(e)=e+$\frac{1+a}{e}$-a<0可得a>$\frac{{e}^{2}+1}{e-1}$,
因为$\frac{{e}^{2}+1}{e-1}$>e-1,
所以a>$\frac{{e}^{2}+1}{e-1}$;
②当1+a≤1,即a≤0时,h(x)在[1,e]上单调递增,
所以h(x)最小值为h(1),由h(1)=1+1+a<0可得a<-2;
③当1<1+a<e,即0<a<e-1时,可得h(x)最小值为h(1+a),
因为0<ln(1+a)<1,
所以,0<aln(1+a)<a
故h(1+a)=2+a-aln(1+a)>2
此时,h(1+a)<0不成立.
综上讨论可得所求a的范围是:a>$\frac{{e}^{2}+1}{e-1}$或a<-2.
点评 本题考查利用导数研究函数的单调性,考查函数存在性问题,考查构造函数思想及分析运算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -5 | C. | -6 | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
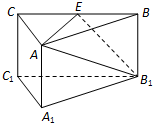 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AC⊥平面ABB1A1 | ||
| C. | A1C1∥平面AB1E | D. | AE,B1C1为异面直线,且AE⊥B1C1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$<x<$\frac{1}{3}$ | B. | x>$\frac{1}{2}$或x<-$\frac{1}{3}$ | C. | x>$\frac{1}{2}$或x<$\frac{1}{3}$ | D. | x>$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p:m≤-2或m≥6;q:y=x2+mx+m+3有两个不同的零点 | |
| B. | p:$\frac{f(-x)}{f(x)}$=1;q:y=f(x)是偶函数 | |
| C. | p:cos α=cos β;q:tan α=tan β | |
| D. | p:A∩B=A;q:A⊆U,B⊆U,∁UB⊆∁UA |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
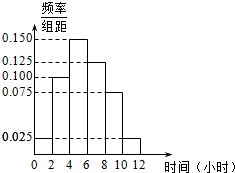 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com