
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)求出函数![]() 的定义域和导数,对实数
的定义域和导数,对实数![]() 分
分![]() 和
和![]() 两种情况讨论,分析导数在区间
两种情况讨论,分析导数在区间![]() 上符号的变化,由此可得出函数
上符号的变化,由此可得出函数![]() 的单调区间;
的单调区间;
(2)证法一:构造函数![]() ,其中
,其中![]() ,利用导数分析得知函数
,利用导数分析得知函数![]() 在区间
在区间![]() 上为减函数,由
上为减函数,由![]() 可得出
可得出![]() ;
;
证法二:分![]() 和
和![]() 时,在
时,在![]() 时,由函数
时,由函数![]() 在
在![]() 上的单调性可得出
上的单调性可得出![]() ,在
,在![]() 时,由(1)中的结论,结合
时,由(1)中的结论,结合![]() 可证明出
可证明出![]() ,综合得出结论.
,综合得出结论.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
若![]() 时,则
时,则![]() ,此时
,此时![]() 在
在![]() 单调递减,
单调递减,
若![]() 时,则由
时,则由![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递增,
单调递增,
综上所述,当![]() 时,
时,![]() 在
在![]() 单调递减;若
单调递减;若![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
(2)证法一:设![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上为减函数,又
上为减函数,又![]() ,所以
,所以![]() ,
,
即![]() ,即
,即![]() ;
;
证法二:由(1)得,当![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
因![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() 在
在![]() 单调递减.
单调递减.
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费(元) |
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
| 0 |
将所抽样本的频率视为概率.
(Ⅰ)求本年度续保人保费的平均值的估计值;
(Ⅱ)按保险合同规定,若续保人在本年度内出险3次,则可获得赔付![]() 元;若续保人在本年度内出险6次,则可获得赔付
元;若续保人在本年度内出险6次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(Ⅲ)续保人原定约了保险公司的销售人员在上午10:30~11:30之间上门签合同,因为续保人临时有事,外出的时间在上午10:45~11:05之间,请问续保人在离开前见到销售人员的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,如图,小卢利用图形的旋转设计某次活动的徽标,他将边长为a的正三角形ABC 绕其中心O逆时针旋转到三角形A1B1C1,且![]() .顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .
.顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .

(1)当=![]() 时,求六边形徽标的面积;
时,求六边形徽标的面积;
(2)求六边形徽标的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() ,
,![]() 的点,直线
的点,直线![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
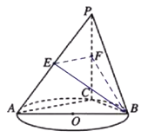
(Ⅰ)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,试判断直线
,试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 大小的取值范围.
大小的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为检查某工厂所生产的8万台电风扇的质量,抽查了其中20台的无故障连续使用时限(单位:小时) 如下:
248 256 232 243 188 268 278 266 289 312
274 296 288 302 295 228 287 217 329 283
分组 | 频数 | 频率 | 频率/组距 |
| |||
| |||
| |||
| |||
| |||
| |||
| |||
| |||
总计 | 0.05 |
(1)完成频率分布表,并作出频率分布直方图;
(2)估计8万台电风扇中有多少台无故障连续使用时限不低于280小时;
(3)用组中值(同一组中的数据在该组区间的中点值)估计样本的平均无故障连续使用时限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①任意两条直线都可以确定一个平面;②若两个平面有3个不同的公共点,则这两个平面重合;③直线a,b,c,若a与b共面,b与c共面,则a与c共面;④若直线l上有一点在平面α外,则l在平面α外.其中错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com