
【题目】对任意m∈[-1,1],函数f(x)=x2+(m-4)x+4-2m的值恒大于零,求x的取值范围.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知圆
中,已知圆 ![]() ,点
,点 ![]() ,点
,点 ![]() ,以B为圆心,
,以B为圆心, ![]() 为半径作圆,交圆C于点P,且
为半径作圆,交圆C于点P,且 ![]() 的平分线交线段CP于点Q.
的平分线交线段CP于点Q.
(1)当a变化时,点Q始终在某圆锥曲线 ![]() 上运动,求曲线
上运动,求曲线 ![]() 的方程;
的方程;
(2)已知直线l过点C,且与曲线 ![]() 交于M,N两点,记
交于M,N两点,记 ![]() 面积为
面积为 ![]() ,
, ![]() 面积为
面积为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)试求图中![]() 的值,并计算区间
的值,并计算区间![]() 上的样本数据的频率和频数;
上的样本数据的频率和频数;
(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到![]() ).
).
注:同一组数据用该组区间的中点值作为代表
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折叠后的线段
,是否存在折叠后的线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )求三棱锥
)求三棱锥![]() 的体积的最大值,并求此时点
的体积的最大值,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 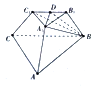
(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() (
(![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴, ![]() 轴上的截距分别为
轴上的截距分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为3![]() 的
的![]() 圆形(
圆形(![]() 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料![]() ,其中点
,其中点![]() 在圆弧上,点
在圆弧上,点![]() 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮![]() 卷成一个以
卷成一个以![]() 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长![]() ,圆柱的体积为
,圆柱的体积为![]() .
.
(1)写出体积![]() 关于
关于![]() 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当![]() 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积![]() 最大?最大体积是多少?(圆柱体积公式:
最大?最大体积是多少?(圆柱体积公式: ![]() ,
, ![]() 为圆柱的底面积,
为圆柱的底面积, ![]() 为圆柱的高)
为圆柱的高)

查看答案和解析>>
科目:高中数学 来源: 题型:
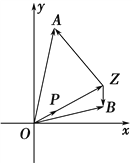
【题目】如图,已知![]() =(2,1),
=(2,1),![]() =(1,7),
=(1,7),![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点.
(1)求使![]() 取最小值时的
取最小值时的![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com