
【题目】已知双曲线![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,并且
,并且![]() 经过点
经过点![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有且仅有一个公共点,求直线
有且仅有一个公共点,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() ,且
,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)过点![]() 作互相垂直的两条直线,分别交曲线
作互相垂直的两条直线,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,若四边形
,若四边形![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年在北京召开的国际数学家大会的会标是以我国古代数学家的弦图为基础设计的.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).设其中直角三角形中较小的锐角为![]() ,且
,且![]() ,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
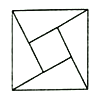
A. 350B. 300C. 250D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
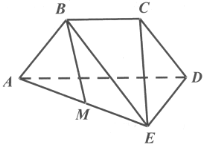
【题目】如图等腰梯形![]() 中
中![]() ,且平面
,且平面 ![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求证:平面 ![]() 平面
平面![]() ;
;
(3)若二面角![]() 的大小为
的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 平行.
平行.
(1)求实数![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上恰有两个零点,求实数
上恰有两个零点,求实数![]() 的取值范围.
的取值范围.
(3)记函数![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com