
【题目】如图,圆![]() 的半径为2,点
的半径为2,点![]() 是圆
是圆![]() 的六等分点中的五个点.
的六等分点中的五个点.

(1)从![]() 中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
(2)在圆![]() 上随机取一点
上随机取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率
的概率
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据直径对直角,用列举法求出基本事件数,计算所求的概率值;
(2)根据三角形的边角关系与面积公式得出点P满足的条件,从而得出所求的概率值.
(1)从![]() 中随机取三点,构成的三角形共10个:
中随机取三点,构成的三角形共10个:
△ABC,△BCD,△ACE,△ADB,△ADC,△ADE,△BEA,△BEC,△BED,△CDE,
记事件M为“从![]() 中随机取三点,这三点构成的三角形是直角三角形”;
中随机取三点,这三点构成的三角形是直角三角形”;
由题意可知以![]() 为端点的线段中,只有
为端点的线段中,只有![]() 是圆O的直径,
是圆O的直径,
所以事件M包含以下6个基本事件:
△ADB,△ADC,△ADE,△BEA,△BEC,△BED,所以所求的概率为![]() ;
;
(2)在Rt△ACD中,AD=4,∠ACD=90°
由题意知![]() 是60°弧,其所对的圆周角∠CAD=30°;
是60°弧,其所对的圆周角∠CAD=30°;
所以CD=2,![]() ;
;
当△PAC的面积大于![]() 时,设点P到AC的距离为d,
时,设点P到AC的距离为d,
则有![]() ,即d>2;
,即d>2;
由题意知四边形ABCD是矩形,
所以AC∥DF,且AC与DF之间的距离为2,
所以点P在![]() 上(不包括点D、F);
上(不包括点D、F);
故所求的概率为![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(2x+![]() )+sin2x.
)+sin2x.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值,并写出f(x)取最大值时x的取值;
(3)设A,B,C为△ABC的三个内角,若cosB=![]() ,f (
,f (![]() )=-
)=-![]() ,且C为锐角,求sinA.
,且C为锐角,求sinA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量与利润的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x/万件 | 10 | 11 | 13 | 12 | 8 | 6 |
利润y/万元 | 22 | 25 | 29 | 26 | 16 | 12 |
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程![]() x+
x+![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O. 
(1)求证:AC⊥OM;
(2)当M为BB1的中点,且θ= ![]() 时,求二面角A﹣D1M﹣B1的余弦值.
时,求二面角A﹣D1M﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
①BD平分∠CBF;
②FB2=FDFA;
③AECE=BEDE;
④AFBD=ABBF.
所有正确结论的序号是( )
A.①②
B.③④
C.①②③
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-1:几何证明选讲]
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.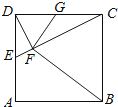
(1)证明:B,C,G,F四点共圆;
(2)若AB=1,E为DA的中点,求四边形BCGF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C1和C2的参数方程分别是 ![]() (φ为参数)和
(φ为参数)和 ![]() (φ为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求圆C1和C2的极坐标方程;
(2)射线OM:θ=a与圆C1的交点为O、P,与圆C2的交点为O、Q,求|OP||OQ|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com