
(满分17分)
已知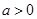 ,函数
,函数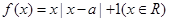 .
.
(1)当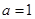 时,求所有使
时,求所有使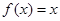 成立的
成立的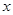 的值;
的值;
(2)当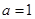 时,求函数
时,求函数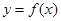 在闭区间
在闭区间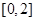 上的最大值和最小值;
上的最大值和最小值;
(3) 试讨论函数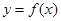 的图像与直线
的图像与直线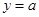 的交点个数.
的交点个数.
(1) 或
或 ;
;
(2)函数的最大值为 ,最小值为
,最小值为
(3)当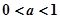 时,函数
时,函数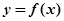 的图像与直线
的图像与直线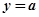 有1个交点;
有1个交点;
当 时,函数
时,函数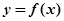 的图像与直线
的图像与直线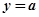 有2个交点;
有2个交点;
当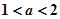 时,函数
时,函数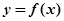 的图像与直线
的图像与直线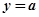 有3个交点;
有3个交点;
当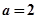 时,函数
时,函数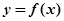 的图像与直线
的图像与直线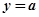 有2个交点;
有2个交点;
当 时,函数
时,函数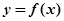 的图像与直线
的图像与直线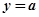 有3个交点
有3个交点
【解析】(1)
所以 或
或 ;....................................5分
;....................................5分
(2)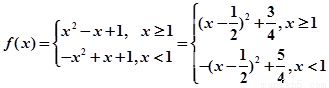 ....................7分
....................7分
结合图像可知函数的最大值为 ,最小值为
,最小值为 ..............10分
..............10分
(3)因为 所以
所以 ,
,
所以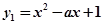 在
在 上递增;.....................................12分
上递增;.....................................12分
 在
在 递增,在
递增,在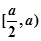 上递减............................13分
上递减............................13分
因为 ,所以当
,所以当 时,函数
时,函数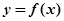 的图像与直线
的图像与直线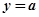 有2个交点;
有2个交点;
又 ,而
,而 ,
,
当且仅当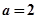 时,上式等号成立.........................................15分
时,上式等号成立.........................................15分
所以,当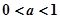 时,函数
时,函数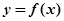 的图像与直线
的图像与直线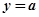 有1个交点;
有1个交点;
当 时,函数
时,函数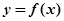 的图像与直线
的图像与直线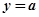 有2个交点;
有2个交点;
当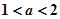 时,函数
时,函数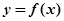 的图像与直线
的图像与直线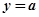 有3个交点;
有3个交点;
当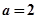 时,函数
时,函数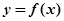 的图像与直线
的图像与直线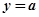 有2个交点;
有2个交点;
当 时,函数
时,函数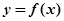 的图像与直线
的图像与直线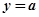 有3个交点.................17分
有3个交点.................17分


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
(2010福建理数)17.(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2011年全国新课标普通高等学校招生统一考试文科数学 题型:解答题
三.解答题(解答应写出文字说明,证明过程或演算步骤):
17. (本小题满分12分)
已知等比数列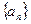 中,
中,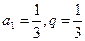 ,
,
(1)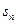 为数列
为数列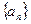 前
前 项的和,证明:
项的和,证明:
(2)设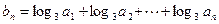 ,求数列
,求数列 的通项公式;
的通项公式;
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高三数学考前热身训练(5) 题型:解答题
(本小题满分17分)已知点 ,
, 和互不相同的点
和互不相同的点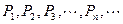 ,满足
,满足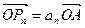
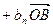
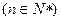 ,其中
,其中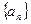 、
、 分别为等差数列和等比数列,
分别为等差数列和等比数列, 为坐标原点,
为坐标原点,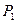 是线段
是线段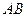 的中点.[来源:学科网ZXXK]
的中点.[来源:学科网ZXXK]
(1) 求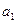 ,
,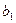 的值;
的值;
(2) 点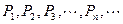 能否在同一条直线上?证明你的结论;
能否在同一条直线上?证明你的结论;
(3) 证明:对于给定的公差不为零的数列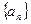 ,都能找到惟一的数列
,都能找到惟一的数列 ,使得
,使得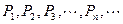 都在一个指数函数的图象上.
都在一个指数函数的图象上.
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省瓦房店市高二下学期期末联考理科数学 题型:解答题
三、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知向量 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  , 若
, 若 ,
,  , 求(1)
, 求(1) ·
· ;
;
(2) .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com