
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数具有性质
,则称函数具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并证明:①
,并证明:①![]() (
(![]() );②
);②![]() ;
;
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() (
(![]() ,
,![]() ),
),
①求证:对任意![]() ,有
,有![]() ;
;
②是否对任意![]() ,均有
,均有![]() ?若有,给出证明,若没有,给出反例.
?若有,给出证明,若没有,给出反例.
【答案】(1)①具有,②不具有,(2)①见解析②不成立
【解析】
(1)①根据已知中函数的解析式,结合指数的运算性质,计算出f(x﹣1)+f(x+1)﹣2f(x)的表达式,进而根据基本不等式,判断其符号即可得到结论;②由y=x3,举出当x=﹣1时,不满足f(x﹣1)+f(x+1)≥2f(x),即可得到结论;
(2)①由于本题是任意性的证明,从下面证明比较困难,故可以采用反证法进行证明,即假设f(i)为f(1),f(2),…,f(n﹣1)中第一个大于0的值,由此推理得到矛盾,进而假设不成立,原命题为真;
②由(2)①中的结论,我们可以举出反例,如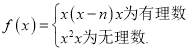 证明对任意x∈[0,n]均有f(x)≤0不成立.
证明对任意x∈[0,n]均有f(x)≤0不成立.
(1)①函数f(x)=ax(a>1)具有性质P.
![]() ,
,
因为a>1,![]() ,
,
即f(x﹣1)+f(x+1)>2f(x),
此函数为具有性质P.
②函数f(x)=x3不具有性质P.
例如,当x=﹣1时,f(x﹣1)+f(x+1)=f(﹣2)+f(0)=﹣8,2f(x)=﹣2,
所以,f(﹣2)+f(0)<f(﹣1),
此函数不具有性质P.
(2)①假设f(i)为f(1),f(2),…,f(n﹣1)中第一个大于0的值,
则f(i)﹣f(i﹣1)>0,
因为函数f(x)具有性质P,
所以,对于任意n∈N*,均有f(n+1)﹣f(n)≥f(n)﹣f(n﹣1),
所以f(n)﹣f(n﹣1)≥f(n﹣1)﹣f(n﹣2)≥…≥f(i)﹣f(i﹣1)>0,
所以f(n)=[f(n)﹣f(n﹣1)]+…+[f(i+1)﹣f(i)]+f(i)>0,
与f(n)=0矛盾,
所以,对任意的i∈{1,2,3,…,n﹣1}有f(i)≤0.
②不成立.
例如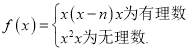
证明:当x为有理数时,x﹣1,x+1均为有理数,f(x﹣1)+f(x+1)﹣2f(x)=(x﹣1)2+(x+1)2﹣2x2﹣n(x﹣1+x+1﹣2x)=2,
当x为无理数时,x﹣1,x+1均为无理数,f(x﹣1)+f(x+1)﹣2f(x)=(x﹣1)2+(x+1)2﹣2x2=2
所以,函数f(x)对任意的x∈R,均有f(x﹣1)+f(x+1)≥2f(x),
即函数f(x)具有性质P.
而当x∈[0,n](n>2)且当x为无理数时,f(x)>0.
所以,在①的条件下,“对任意x∈[0,n]均有f(x)≤0”不成立.


科目:高中数学 来源: 题型:
【题目】随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,SF快递收取快递费的标准是:重量不超过1kg的包裹收费10元;重量超过1kg的包裹,在收费10元的基础上,每超过1kg(不足1kg,按1kg计算)需再收5元.某县SF分代办点将最近承揽的100件包裹的重量统计如下:
重量(单位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件数 | 43 | 30 | 15 | 8 | 4 |
对近60天,每天揽件数量统计如下表:
件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件数 | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 1 | 6 |
以上数据已做近似处理,将频率视为概率.
(1)计算该代办未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数如下表所示:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x(℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻的2组数据的概率.
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求y关于x的线性回归方程![]() .
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】昆明市某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300),该社团将该校区在2018年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图4,把该直方图所得频率估计为概率.
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4度中度污染 | 5度重度污染 | 6级严重污染 |
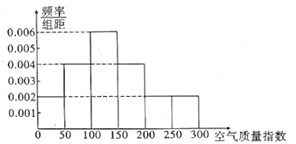
(1)请估算2019年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(2)用分层抽样的方法共抽取10天,则空气质量指数在![]() ,
,![]() ,
,![]() 的天数中各应抽取几天?
的天数中各应抽取几天?
(3)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元若在(2)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用
的天数中任意抽取两天,求这两天的净化空气总费用![]() 的分布列
的分布列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。
(1)求曲线![]() 的极坐标方程和直线l的直角坐标方程;
的极坐标方程和直线l的直角坐标方程;
(2)设直线l与曲线![]() 交于不同的两点A,B,点M为抛物线
交于不同的两点A,B,点M为抛物线![]() 的焦点,求
的焦点,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com