
【题目】设函数![]() .
.
(1)若当![]() 时,函数
时,函数![]() 的图象恒在直线
的图象恒在直线![]() 上方,求实数
上方,求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
试题分析:(1)令![]() ,只要满足对任意
,只要满足对任意![]() 都有
都有![]() ,对
,对![]() 分情况讨论即可;
分情况讨论即可;
(2)对要证明的不等式等价变形,结合(1)中结论即可得证.
试题解析:(Ⅰ)令![]() ,则
,则![]() ,
,![]() ,
,![]()
①当![]() 时,由于
时,由于![]() ,有
,有![]() ,
,
于是![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() ,因此
,因此![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ;
;
②当![]() 时,由于
时,由于![]() ,有
,有![]() ,
,
于是![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() ,
,
因此![]() 在
在![]() 上单调递减,即
上单调递减,即![]() 不符;
不符;
③当![]() 时,令
时,令![]() ,当
,当![]() 时,
时,
![]() ,于是
,于是![]() 在
在![]() 上单调递减,
上单调递减,
从而![]() ,因此
,因此![]() 在
在![]() 上单调递减,
上单调递减,
即![]() 而且仅有
而且仅有![]() 不符.
不符.
综上可知,所求实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)对要证明的不等式等价变形如下:
对于任意的正整数![]() ,不等式
,不等式![]() 恒成立,等价变形
恒成立,等价变形
![]() 相当于(2)中
相当于(2)中![]() ,
,![]() 的情形,
的情形,
![]() 在
在![]() 上单调递减,即
上单调递减,即![]() ;
;
取![]() ,得:都有
,得:都有![]() 成立;
成立;
令![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上的点,且AM=BN,将三角形ADE沿AE折起,则下列说法正确的是 (填上所有正确说法的序号).
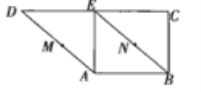
①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;
②不论D折至何位置都有MN⊥AE;
③不论D折至何位置(不在平面ABC内)都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市一汽车出租公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆,分别统计了每辆车某个星期内的出租天数,统计数据如下表:
A车型 B车型
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 | 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅰ)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)
(ⅰ)试写出A,B两种车型的出租天数的分布列及数学期望;
(ⅱ)如果两种车辆每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆(注:两种车型的采购价格相当),请你根据所学的统计知识,建议应该购买哪一种车型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;

(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动点![]() 到定点
到定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离
的距离
之比是常数![]() ,记动点
,记动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() ,与轨迹
,与轨迹![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,与轨迹
,与轨迹![]() 是否存在点
是否存在点![]() ,使得四边形
,使得四边形![]() 为菱形?若存在,请求出直线
为菱形?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最后一位选手的成绩.
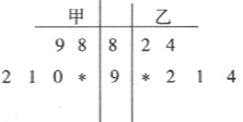
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.请你从平均分和方差的角度来分析两个班的选手的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过抛物线上一点
,过抛物线上一点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的形状,并求抛物线
的形状,并求抛物线![]() 的方程;
的方程;
(2)若![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,其中点
,其中点![]() ,若抛物线
,若抛物线![]() 上存在异于
上存在异于![]() 的点
的点![]() ,使得经过
,使得经过![]() 三点的圆和抛物线在点
三点的圆和抛物线在点![]() 处有相同的切线,求点
处有相同的切线,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|-2≤x≤10},Q={x|1-m≤x≤1+m}.
(1)求集合RP;
(2)若PQ,求实数m的取值范围;
(3)若P∩Q=Q,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com