【题目】近年来，我国电子商务蓬勃发展，有关部门推出了针对网购平台的商品和服务的评价系统，从该系统中随机选出100名交易者，并对其交易评价进行了统计，网购者对商品的满意率为0.6，对服务的满意率为0.75，其中对商品和服务都满意的有40人.
（1）根据已知条件完成下面的
列联表，并回答能否有
的把握认为“网购者对服务满意与对商品满意之间有关”？
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
（2）若对商品和服务都不满意者的集合为
.已知
中有2名男性，现从
中任取2人调查其意见.求取到的2人恰好是一男一女的概率.
附：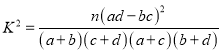 
(其中
为样本容量）
|
|
|
|
|
|
|
|
|
|
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案科目：高中数学 来源： 题型：
【题目】在空间中，过点A作平面π的垂线，垂足为B，记B=fπ（A）．设α，β是两个不同的平面，对空间任意一点P，Q1=fβ[fα（P）]，Q2=fα[fβ（P）]，恒有PQ1=PQ2，则（ ）
A．平面α与平面β垂直
B．平面α与平面β所成的（锐）二面角为45°
C．平面α与平面β平行
D．平面α与平面β所成的（锐）二面角为60°
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
的离心率为
，椭圆C的四个顶点围成的四边形的面积为
．
求椭圆C的方程；
直线l与椭圆C交于
，
两个不同点，O为坐标原点，若
的面积为
，证明：
为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度
（单位：千克/年）是养殖密度
（单位：尾/立方米）的函数.当
时，的值为2千克/年；当
时，是的一次函数；当
时，因缺氧等原因，的值为0千克/年.
（1）当
时，求关于的函数表达式.
（2）当养殖密度为多少时，鱼的年生长量（单位：千克/立方米）可以达到最大？并求出最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)=
g(x)=f(x)+
x-6lnx,其中
R.
(1)当=1时,判断f(x)的单调性;
(2)当=2时,求出g(x)在（0,1）上的最大值；
(3)设函数
当=2时,若
总有
成立,求实数m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的右焦点为
，且过点
求椭圆的标准方程；
设直线l：
与椭圆在第一象限的交点为M，过点F且斜率为
的直线与l交于点N，若
与
的面积之比为3：
为坐标原点
，求k的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一只小蜜蜂位于数轴上的原点处，小蜜蜂每一次具有只向左或只向右飞行一个单位或者两个单位距离的能力，且每次飞行至少一个单位.若小蜜蜂经过5次飞行后，停在数轴上实数3位于的点处，则小蜜蜂不同的飞行方式有多少种？（ ）
A. 5 B. 25 C. 55 D. 75
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）
已知椭圆
：
的左、右顶点分别为A，B，其离心率
，点
为椭圆上的一个动点，
面积的最大值是
．
(1)求椭圆的方程；
(2)若过椭圆右顶点
的直线
与椭圆的另一个交点为
，线段
的垂直平分线与
轴交于点
，当
时，求点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
