
【题目】已知![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设![]() .
.
(i)若函数![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大值;
的最大值;
(ii)当![]() 时,判断函数
时,判断函数![]() 有几个零点,并给出证明.
有几个零点,并给出证明.
【答案】(Ⅰ)1;(Ⅱ)![]() 1;
1;![]() 详见解析.
详见解析.
【解析】
![]() Ⅰ
Ⅰ![]() 求函数
求函数![]() 的导数
的导数![]() ,计算
,计算![]() 时的导数即可求出a的值;
时的导数即可求出a的值;![]() Ⅱ
Ⅱ![]() 求
求![]() 的导数
的导数![]() ,讨论当
,讨论当![]() 和
和![]() 时
时![]() 的单调性,由单调性判断最值即可得到b的最大值;
的单调性,由单调性判断最值即可得到b的最大值;![]() 化简
化简![]() 知0是
知0是![]() 的一个零点,利用构造函数法讨论
的一个零点,利用构造函数法讨论![]() 和
和![]() 时,函数
时,函数![]() 是否有零点,从而确定函数
是否有零点,从而确定函数![]() 的零点情况.
的零点情况.
解:![]() Ⅰ
Ⅰ![]() 函数
函数![]() ,则
,则![]() ,
,
由题意知![]() 时,
时,![]() ,即a的值为1;
,即a的值为1;
![]() Ⅱ
Ⅱ![]() ,
,
所以![]() ,
,
当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() ,
,![]() 单调递增,所以
单调递增,所以![]() ;
;
当![]() 时,若
时,若![]() ,令
,令![]() ,解得
,解得![]() 舍去
舍去![]() ,
,![]() ,
,
所以![]() 在
在![]() 内单调递减,
内单调递减,![]() ,所以
,所以![]() 不恒成立,
不恒成立,
所以b的最大值为1;
![]() ,显然
,显然![]() 有一个零点为0,
有一个零点为0,
设![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() 无零点,所以
无零点,所以![]() 只有一个零点0;
只有一个零点0;
当![]() 时,
时,![]() ,所以
,所以![]() 在R上单调递增,
在R上单调递增,
又![]() ,
,![]() ,
,
由零点存在性定理可知,![]() 在
在![]() 上有唯一一个零点
上有唯一一个零点![]() ,
,
所以![]() 有2个零点;
有2个零点;
综上所述,![]() 时,
时,![]() 只有一个零点,
只有一个零点,![]() 时,
时,![]() 有2个零点.
有2个零点.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .判定直线
.判定直线![]() 的斜率是否依次构成等差数列?并说明理由.
的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
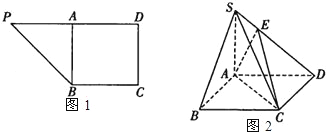
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,如图
的中点,如图![]() 将
将![]() 沿
沿![]() 折到
折到![]() 的位置,使
的位置,使![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,如图2.
,如图2.
![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 求二面角
求二面角![]() 的正切值;
的正切值;
![]() 在线段
在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 的离心率是
的离心率是![]() ,
,![]() ,
,![]() 分别为椭圆E的左右顶点,B为上顶点,
分别为椭圆E的左右顶点,B为上顶点,![]() 的面积为
的面积为![]() 直线l过点
直线l过点![]() 且与椭圆E交于P,Q两点.
且与椭圆E交于P,Q两点.

![]() 求椭圆E的标准方程;
求椭圆E的标准方程;
![]() 求
求![]() 面积的最大值;
面积的最大值;
![]() 设直线
设直线![]() 与直线
与直线![]() 交于点N,证明:点N在定直线上,并写出该直线方程.
交于点N,证明:点N在定直线上,并写出该直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项正确的为( )
A.已知直线![]() :
:![]() ,
,![]() :
:![]() ,则
,则![]() 的充分不必要条件是
的充分不必要条件是![]()
B.命题“若数列![]() 为等比数列,则数列
为等比数列,则数列![]() 为等比数列”是假命题
为等比数列”是假命题
C.棱长为![]() 正方体
正方体![]() 中,平面
中,平面![]() 与平面
与平面![]() 距离为
距离为![]()
D.已知![]() 为抛物线
为抛物线![]() 上任意一点且
上任意一点且![]() ,若
,若![]() 恒成立,则
恒成立,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.
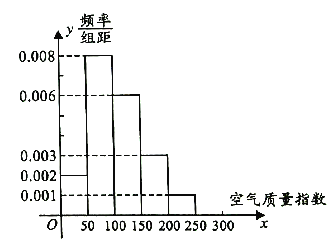
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为![]() ,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() .
.
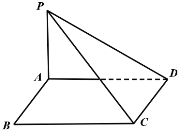
(1)问当实数![]() 在什么范围时,
在什么范围时,![]() 边上能存在点
边上能存在点![]() ,使得
,使得![]() ?
?
(2)当![]() 边上有且仅有一个点
边上有且仅有一个点![]() 使得
使得![]() 时,求二面角
时,求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
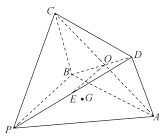
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为平面
为平面![]() 内任一点.
内任一点.
(1)在平面![]() 内,过
内,过![]() 点是否存在直线
点是否存在直线![]() 使
使![]() ?如果不存在,请说明理由,如果存在,请说明作法;
?如果不存在,请说明理由,如果存在,请说明作法;
(2)过![]() ,
, ![]() ,
, ![]() 三点的平面将几何体
三点的平面将几何体![]() 截去三棱锥
截去三棱锥![]() ,求剩余几何体
,求剩余几何体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com