
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 、
、![]() 的交点记为
的交点记为![]() .
.
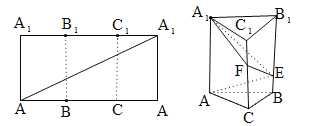
(1)在三棱柱![]() 中,若过
中,若过![]() 三点做一平面,求截得的几何体
三点做一平面,求截得的几何体![]() 的表面积;
的表面积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() :
:![]() 上任意一点,
上任意一点,![]() ,线段
,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 交于点
交于点![]() ,当点
,当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)记曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() 是直线
是直线![]() 上任意一点,直线
上任意一点,直线![]() ,
,![]() 与曲线
与曲线![]() 的另一个交点分别为
的另一个交点分别为![]() ,求证:直线
,求证:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,函数![]() 在第一象限内的图像如图所示,试做如下操作:把x轴上的区间
在第一象限内的图像如图所示,试做如下操作:把x轴上的区间![]() 等分成n个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
等分成n个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数![]() 的图像上.若用
的图像上.若用![]() 表示第k个矩形的面积,
表示第k个矩形的面积,![]() 表示这n个叫矩形的面积总和.
表示这n个叫矩形的面积总和.
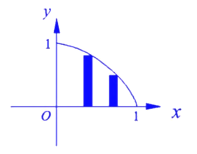
(1)求![]() 的表达式;
的表达式;
(2)利用数学归纳法证明![]() ,并求出
,并求出![]() 的表达式
的表达式
(3)求![]() 的值,并说明
的值,并说明![]() 的几何意义.
的几何意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其中
,其中![]() ,点
,点![]() 是椭圆
是椭圆![]() 的右顶点,射线
的右顶点,射线![]() :
:![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设椭圆![]() 的长半轴、短半轴的长分别为
的长半轴、短半轴的长分别为![]() 、
、![]() ,当
,当![]() 的值在区间
的值在区间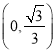 中变化时,求
中变化时,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,以![]() 为焦点,
为焦点,![]() 为顶点且开口方向向左的抛物线过点
为顶点且开口方向向左的抛物线过点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司航拍宣传画报,为了凸显公司文化,选择如图所示的边长为2百米的正三角形![]() 空地进行布置拍摄场景,在
空地进行布置拍摄场景,在![]() 的中点
的中点![]() 处安装中央聚光灯,
处安装中央聚光灯,![]() 为边
为边![]() 上得可以自由滑动的动点,其中
上得可以自由滑动的动点,其中![]() 设置为普通色彩灯带(灯带长度可以自由伸缩),线段
设置为普通色彩灯带(灯带长度可以自由伸缩),线段![]() 部分需要材料
部分需要材料![]() (单位:百米)装饰用以增加拍摄效果因材料
(单位:百米)装饰用以增加拍摄效果因材料![]() 价格昂贵,所以公司要求采购
价格昂贵,所以公司要求采购![]() 材料使用不造成浪费.
材料使用不造成浪费.
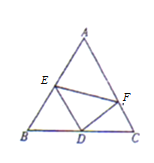
(1)当![]() ,
,![]() 与
与![]() 垂直时,采购部需要采购多少百米材料
垂直时,采购部需要采购多少百米材料![]() ?
?
(2)为了增加拍摄动态效果需要,现要求点![]() 在
在![]() 边上滑动,且
边上滑动,且![]() ,则购买材料
,则购买材料![]() 的范围是多少才能满足动态效果需要又不会造成浪费.
的范围是多少才能满足动态效果需要又不会造成浪费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义:如果实数![]() 满足
满足![]() , 那么称
, 那么称![]() 比
比![]() 更接近
更接近![]() .对于(2)中的
.对于(2)中的![]() 及
及![]() ,问:
,问:![]() 和
和![]() 哪个更接近
哪个更接近![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,若函数
,若函数![]() 满足:
满足:![]() ,都有
,都有![]() ,就称这个函数是点
,就称这个函数是点![]() 的“限定函数”.以下函数:①
的“限定函数”.以下函数:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中是原点
,其中是原点![]() 的“限定函数”的序号是______.已知点
的“限定函数”的序号是______.已知点![]() 在函数
在函数![]() 的图象上,若函数
的图象上,若函数![]() 是点
是点![]() 的“限定函数”,则
的“限定函数”,则![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是抛物线C:y2=2px(p>0)的焦点,若点P(x0,4)在抛物线C上,且![]() .
.
(1)求抛物线C的方程;
(2)动直线l:x=my+1(m![]() R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com