
【题目】以下说法中正确的是______.
①函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
②函数![]() 的图象过定点
的图象过定点![]() ;
;
③若![]() 是函数
是函数![]() 的零点,且
的零点,且![]() ,则
,则![]() ;
;
④方程![]() 的解是
的解是![]() ;
;
⑤命题“![]() ,
,![]() ”的否定是
”的否定是![]() ,
,![]() .
.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
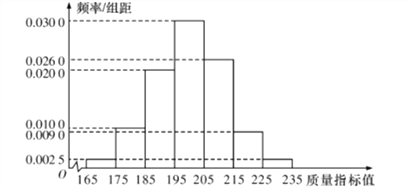
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中为真命题的是( )
A.命题“若![]() ,则
,则![]() ”的否命题
”的否命题
B.命题“若x>y,则x>|y|”的逆命题
C.命题“若x=1,则![]() ”的否命题
”的否命题
D.命题“已知![]() ,若
,若![]() ,则a>b”的逆命题、否命题、逆否命题均为真命题
,则a>b”的逆命题、否命题、逆否命题均为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)当![]() 时,若
时,若![]() 是函数
是函数![]() 的极值点,求证:
的极值点,求证:![]() ;
;
(2)(i)求证:当![]() 时,
时,![]() ;
;
(ii)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
注:e=2.71828...为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求常数![]() 的值;
的值;
(2)判断并用定义法证明函数的单调性;
(3)函数![]() 的图象由函数
的图象由函数![]() 的图象先向右平移
的图象先向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得到,写出
个单位得到,写出![]() 的一个对称中心,若
的一个对称中心,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若残差平方和越小,则相关指数![]() 越小
越小
B.将一组数据中每一个数据都加上或减去同一常数,方差不变
C.若![]() 的观测值越大,则判断两个分类变量有关系的把握程度越小
的观测值越大,则判断两个分类变量有关系的把握程度越小
D.若所有样本点均落在回归直线上,则相关系数![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环境指数是“宜居城市”评比的重要指标,根据以下环境指数的数据,对名列前20名的“宜居城市”的环境指数进行分组统计,结果如表所示,现从环境指数在![]() 和
和![]() 内的“宜居城市”中随机抽取2个市进行调研,则至少有1个市的环境指数在
内的“宜居城市”中随机抽取2个市进行调研,则至少有1个市的环境指数在![]() 的概率为( )
的概率为( )
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com