
【题目】设函数f(x)=x﹣x2+3lnx.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)证明:曲线y=f(x)在直线y=2x﹣2的下方(除点![]() 外).
外).
【答案】(Ⅰ)极大值3ln![]() ;无极小值; (Ⅱ)见解析.
;无极小值; (Ⅱ)见解析.
【解析】
(Ⅰ)求导后,得到函数的单调性,根据单调性可求得极值;
(Ⅱ)令g(x)=f(x)﹣2x+2=﹣x2﹣x+2+3lnx,(x>0),转化为证明![]() ,利用导数求得最大值即可证明结论.
,利用导数求得最大值即可证明结论.
(Ⅰ)f(x)的定义域是(0,+∞),f′(x)=1﹣2x![]() ,
,
令f′(x)>0,解得:0<x![]() ,令f′(x)<0,解得:x
,令f′(x)<0,解得:x![]() ,
,
故f(x)在(0,![]() )递增,在(
)递增,在(![]() ,+∞)递减,
,+∞)递减,
故f(x)极大值=f(![]() )
)![]() 3ln
3ln![]() 3ln
3ln![]() ;无极小值;
;无极小值;
(Ⅱ)令g(x)=f(x)﹣2x+2=﹣x2﹣x+2+3lnx,(x>0),
g′(x)=﹣2x﹣1![]() ,
,
令g′(x)>0,解得:0<x<1,令g′(x)<0,解得:x>1,
故g(x)在(0,1)递增,在(1,+∞)递减,
故g(x)max=g(1)=﹣1﹣1+2+3ln1=0,
故曲线y=f(x)在直线y=2x﹣2的下方(除点![]() 外).
外).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
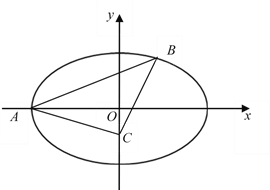
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左顶点为
的左顶点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 为
为![]() 轴上的一点.
轴上的一点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,求直线
为直角顶点的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高城市居民生活幸福感,某城市公交公司大力确保公交车的准点率,减少居民乘车候车时间为此,该公司对某站台乘客的候车时间进行统计乘客候车时间受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,乘客候车时间随机变量![]() 满足正态分布
满足正态分布![]() 在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图频率分布直方图.
在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图频率分布直方图.
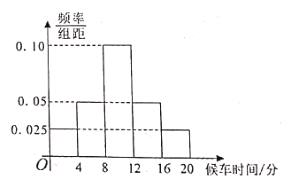
(1)在直方图各组中,以该组区间的中点值代表该组中的各个值,试估计![]() 的值;
的值;
(2)在统计学中,发生概率低于千分之三的事件叫小概率事件,一般认为,在正常情况下,一次试验中,小概率事件是不能发生的在交通拥堵情况正常、非节假日的某天,随机调查了该站的10名乘客的候车时间,发现其中有3名乘客候车时间超过15分钟,试判断该天公交车准点率是否正常,说明理由.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() :
:![]() (参数
(参数![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为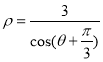 ,点
,点![]() 的极坐标为
的极坐标为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,并求出点
的极坐标方程化为直角坐标方程,并求出点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 中点
中点![]() 到曲线
到曲线![]() 上的点的距离的最小值.
上的点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点E、F、G分别为棱A1D1、A1A、A1B1的中点,给出下列四个命题:①EF⊥B1C;②BC1∥平面EFG;③A1C⊥平面EFG;④异面直线FG、B1C所成角的大小为![]() .其中正确命题的序号为( )
.其中正确命题的序号为( )
A.①②B.②③C.①②③D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉某科技公司为提高市场销售业绩,现对某产品在部分营销网点进行试点促销活动.现有两种活动方案,在每个试点网点仅采用一种活动方案,经统计,2018年1月至6月期间,每件产品的生产成本为10元,方案1中每件产品的促销运作成本为5元,方案2中每件产品的促销运作成本为2元,其月利润的变化情况如图①折线图所示.

(1)请根据图①,从两种活动方案中,为该公司选择一种较为有利的活动方案(不必说明理由);
(2)为制定本年度该产品的销售价格,现统计了8组售价xi(单位:元/件)和相应销量y(单位:件)(i=1,2,…8)并制作散点图(如图②),观察散点图可知,可用线性回归模型拟合y与x的关系,试求y关于x的回归方程(系数精确到整数);
参考公式及数据:![]() 40,
40,![]() 660,
660,![]() xiyi=206630,
xiyi=206630,![]() x
x![]() 12968,
12968,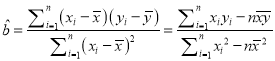 ,
,![]() ,
,
(3)公司策划部选![]() 1200lnx+5000和
1200lnx+5000和![]() ═
═![]() x3+1200两个模型对销量与售价的关系进行拟合,现得到以下统计值(如表格所示):
x3+1200两个模型对销量与售价的关系进行拟合,现得到以下统计值(如表格所示):
|
| |
| 52446.95 | 122.89 |
| 124650 | |
相关指数 | R | R |
相关指数:R2=1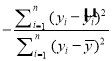 .
.
(i)试比较R12,R22的大小(给出结果即可),并由此判断哪个模型的拟合效果更好;
(ii)根据(1)中所选的方案和(i)中所选的回归模型,求该产品的售价x定为多少时,总利润z可以达到最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
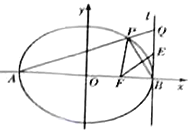
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() .右焦点为
.右焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,设直线
,设直线![]() ,延长
,延长![]() 交直线
交直线![]() 于点
于点![]() ,线段的
,线段的![]() 中点为
中点为![]() ,求证:点
,求证:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上
上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com