
【题目】如图,已知![]() =(2,1),
=(2,1),![]() =(1,7),
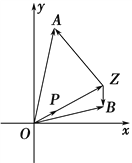
=(1,7),![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点.
(1)求使![]() 取最小值时的
取最小值时的![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
【答案】(1)最小值-8,![]() = (4,2)(2)
= (4,2)(2)![]()
【解析】分析:(1)运用向量共线的坐标表示,求得向量ZA,ZB的坐标,由数量积的标准表示,结合二次函数的最值求法,可得最小值,及向量OZ;(2)求得t=2的向量ZA,ZB,以及模的大小,由向量的夹角公式,计算即可得到.
详解:(1)∵Z是直线OP上的一点,∴![]() ∥
∥![]() .
.
设实数t,使![]() =t
=t![]() ,∴
,∴![]() =t(2,1)=(2t,t),
=t(2,1)=(2t,t),
则![]() =
=![]() -
-![]() =(1,7)-(2t,t)=(1-2t,7-t),
=(1,7)-(2t,t)=(1-2t,7-t),
![]() =
=![]() -
-![]() =(5,1)-(2t,t)=(5-2t,1-t).
=(5,1)-(2t,t)=(5-2t,1-t).
∴![]() ·
·![]() =(1-2t)(5-2t)+(7-t)(1-t)=5t2-20t+12=5(t-2)2-8.
=(1-2t)(5-2t)+(7-t)(1-t)=5t2-20t+12=5(t-2)2-8.
当t=2时,![]() ·
·![]() 有最小值-8,此时
有最小值-8,此时![]() =(2t,t)=(4,2).
=(2t,t)=(4,2).
(2)当t=2时,![]() =(1-2t,7-t)=(-3,5),
=(1-2t,7-t)=(-3,5),
|![]() |=
|=![]() ,
,![]() =(5-2t,1-t)=(1,-1),|
=(5-2t,1-t)=(1,-1),|![]() |=
|=![]() .
.
故cos∠AZB=![]() =
=![]() =-
=-![]() =-
=-![]()


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是平面,
是平面,![]() ,
,![]() 是直线,给出下列命题:
是直线,给出下列命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③如果![]() ,
,![]() ,
,![]() ,
,![]() 是异面直线,则
是异面直线,则![]() 与
与![]() 相交;
相交;
④若![]() .
.![]() ,且
,且![]() ,
,![]() ,则
,则![]() ,且
,且![]()
其中正确确命题的序号是_____(把正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ? 若存在,求出符合条件的所有
? 若存在,求出符合条件的所有![]() 的值构成的集合
的值构成的集合![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
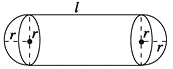
【题目】某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为![]() 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
①写出y关于r的函数表达式,并求该函数的定义域;
②求该容器的建造费用最小时的r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 点
点![]() ,
, ![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() 。
。
(Ⅰ)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)直线![]() 与点
与点![]() 的轨迹交于不同两点
的轨迹交于不同两点![]() 和
和![]() ,且
,且![]() (其中 O 为坐标
(其中 O 为坐标
原点),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用![]() 这六个数字.
这六个数字.
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为![]() 的倍数的五位数?
的倍数的五位数?
(3)能组成多少个无重复数字且比![]() 大的四位数?
大的四位数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com