
(1)求证:AM∥平面BDE;
(2)求证:AM⊥平面BDF;
(3)求二面角A-DF-B的大小.

证明:(1)建立如下图所示的空间直角坐标系.

设AC∩BD=N,连接NE,
则点N、E的坐标分别是(![]() ,
,![]() ,0)、(0,0,1),
,0)、(0,0,1),
∴![]() =(-
=(-![]() ,-
,-![]() ,1).
,1).
又点A、M的坐标分别是(![]() ,
,![]() ,0)、(
,0)、(![]() ,
,![]() ,1),
,1),
∴![]() =(-
=(-![]() ,-
,-![]() ,1).
,1).
∴![]() =
=![]() 且
且![]() 与
与![]() 不共线.
不共线.
∴NE∥AM.
又∵NE![]() 平面BDE,AM
平面BDE,AM![]() 平面BDE,
平面BDE,
∴AM∥平面BDE;
(2)![]() =(-
=(-![]() ,-
,-![]() ,1),
,1),
∵D(2,0,0),F(![]() ,
,![]() ,1),
,1),
∴![]() =(0,
=(0,![]() ,1).
,1).
∴![]() ·
·![]() =0.
=0.
∴![]() ⊥
⊥![]() .
.
同理![]() ⊥
⊥![]() .
.
又DF∩BF=F,
∴AM⊥平面BDF.
解析:(3)∵AF⊥AB,AB⊥AD,AF∩AD=A,
∴AB⊥平面ADF.
∴![]() =(-
=(-![]() ,0,0)为平面DAF的法向量.
,0,0)为平面DAF的法向量.
∵![]() ·
·![]() =(-
=(-![]() ,-
,-![]() ,1)·(-
,1)·(-![]() ,
,![]() ,0)=0,
,0)=0,![]() ·
·![]() =(-
=(-![]() ,-
,-![]() ,1)·(
,1)·(![]() ,
,![]() ,1)=0得
,1)=0得![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() 为平面BDF的法向量.
为平面BDF的法向量.
∴cos(![]() ,
,![]() )=
)= ![]() .
.
∴![]() 与
与![]() 的夹角是60°.
的夹角是60°.
即所求二面角A-DF-B的大小是60°.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:044
如下图,已知正方形ABCD的边长等于1,设![]() =a,
=a,![]() =b,
=b,![]() =c,求作向量a+b+c,并计算|a+b+c|.
=c,求作向量a+b+c,并计算|a+b+c|.
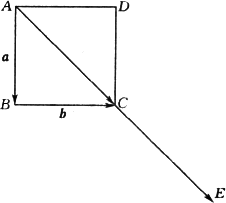
查看答案和解析>>
科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:044
如下图,已知正方形ABCD的边长等于1,设![]() =a,
=a,![]() =b,
=b,![]() =c,求作向量.
=c,求作向量.
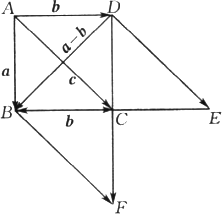
(1)a-b-c,并求|a-b+c|;
(2)a-b-c,并求|a-b-c|.
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2006
福州模拟)如下图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,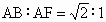 ,M为线段EF的中点.
,M为线段EF的中点.
(1)
求证:AM⊥平面BDF;(2)
求二面角A-DF-B的大小.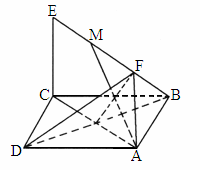
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com