
【题目】已知![]() .
.
(1)若![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)若关于x的方程![]() 有两个不同的解,求实数a的取值范围.
有两个不同的解,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用等价转化,求解![]() 的最大值即可;
的最大值即可;
(2)把![]() 的解的情况等价转化为
的解的情况等价转化为![]() 有两解,结合图象变化趋势可求.
有两解,结合图象变化趋势可求.
(1)因为![]() .
.
若x≤0时,f(x)≤0,g(x)>0,f(x)≤g(x)恒成立;
若x>0,f(x)≤g(x)恒成立等价为![]() ,
,
即![]() ,即有
,即有![]() ,
,
设![]() ,
, ![]() ,
,
令![]() ,
,
可得![]() 在x>0递减,当x>1时,
在x>0递减,当x>1时,![]() ,即
,即![]() ,
,![]() 在x>1递减;
在x>1递减;
当0<x<1时,![]() ,即
,即![]() ,
,![]() 在0<x<1递增,
在0<x<1递增,
则![]() 在x=1处取得极大值,且为最大值1,
在x=1处取得极大值,且为最大值1,![]() ,
,
所以![]() .
.
(2)若x≤0时,![]() ,
,![]() 无解;
无解;
当x>0时,![]() 恒成立等价为
恒成立等价为![]() ,
,
即![]() ,即有
,即有![]() 有两解,
有两解,
设![]() ,
,
由(1)可知![]() 在x=1处取得极大值,且为最大值1,
在x=1处取得极大值,且为最大值1,![]() ,
,
且![]() ,
,![]() ,当
,当![]() ,
,
可得0<a<1时,关于x的方程![]() 有两个不同的解,
有两个不同的解,
故a的范围是![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】某生物探测器在水中逆流行进时,所消耗的能量为E=cvnT,其中v为行进时相对于水的速度,T为行进时的时间(单位:h),c为常数,n为能量次级数,如果水的速度为4km/h,该生物探测器在水中逆流行进200km.
(1)求T关于v的函数关系式;
(2)①当能量次级数为2时,求探测器消耗的最少能量;
②当能量次级数为3时,试确定v的大小,使该探测器消耗的能量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边长分别为a、b、c,且acosB+bcosA=2ccosB.
(1)若a=3,![]() ,求c的值;
,求c的值;
(2)若![]() ,求f(A)的取值范围.
,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|
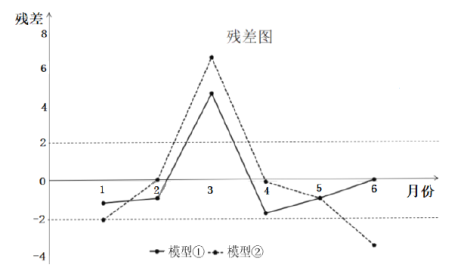
(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程;
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
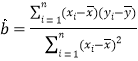
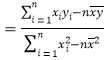 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中.直线1的参数方程为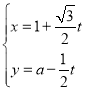 (t为参数).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=2cosθ.
(t为参数).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=2cosθ.
(1)若曲线C关于直线l对称,求a的值;
(2)若A、B为曲线C上两点.且∠AOB![]() ,求|OA|+|OB|的最大值.
,求|OA|+|OB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
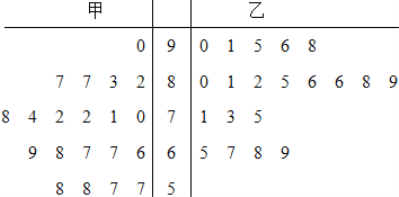
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解高一新生是否愿意参加军训,随机调查了80名新生,得到如下2×2列联表
愿意 | 不愿意 | 合计 | |
男 | x | 5 | M |
女 | y | z | 40 |
合计 | N | 25 | 80 |
(1)写出表中x,y,z,M,N的值,并判断是否有99.9%的把握认为愿意参加军训与性别有关;
(2)在被调查的不愿意参加军训的学生中,随机抽出3人,记这3人中男生的人数为ξ,求ξ的分布列和数学期望.
参考公式: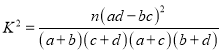
附:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的两交点间距离为
的两交点间距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,设![]() 是椭圆
是椭圆![]() 上的一动点,由原点
上的一动点,由原点![]() 向圆
向圆![]() 引两条切线,分别交椭圆
引两条切线,分别交椭圆![]() 于点
于点![]() ,若直线
,若直线![]() 的斜率均存在,并分别记为
的斜率均存在,并分别记为![]() ,求证:
,求证:![]() 为定值.
为定值.
(3)在(2)的条件下,试问![]() 是否为定值?若是,求出该值;若不是,请说明理由.
是否为定值?若是,求出该值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com