
分析 由条件利用正切函数的定义域和值域求得tanx的范围,再利用二次函数的性质求得函数y的值域.
解答 解:由x∈[-$\frac{π}{4}$,$\frac{π}{3}$],可得tanx∈[-1,$\sqrt{3}$],函数y=-tan2x-tanx-3=-${(tanx+\frac{1}{2})}^{2}$-$\frac{11}{4}$,
故当tanx=-$\frac{1}{2}$时,函数y取得最大值为-$\frac{11}{4}$,当tanx=$\sqrt{3}$时,函数y取得最小值为-6-2$\sqrt{3}$,
故函数y的值域为[-6-2$\sqrt{3}$,-$\frac{11}{4}$].
点评 本题主要考查正切函数的定义域和值域,二次函数的性质应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
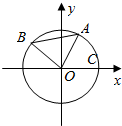 已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α
已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}•\overrightarrow{b}$=0($\overrightarrow{a}$≠0,$\overrightarrow{b}$≠0),则$\overrightarrow{a}⊥\overrightarrow{b}$ | B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若ac2>bc2,则a>b | D. | 若α=60°,则cosα=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com