
t
∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0),问:①直线PQ是否能通过点M(6,1)和N(4,5);②在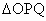 内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.
内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.
(1)
求证:顶点C一定在直线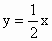 上;
上;
(2)
求图中阴影部分面积的最大值,并求此时顶点A、B、C、D的坐标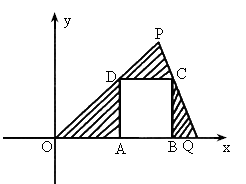
|
①由两点式可得直线 PQ的方程为
假设点 M在PQ上,则有
∴ M不在PQ上.同理得: 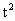 -16t+50=0得 -16t+50=0得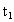 =8- =8-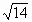 , ,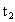 =8+ =8+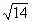 (舍去)[∵t∈(0,10)] (舍去)[∵t∈(0,10)]
当 t=8-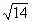 时,直线PQ过点N(4,5). 时,直线PQ过点N(4,5).
②由已知可设 A(a,0)、B(2a,0)、C(2a,a)、D(a,a)(1) 由C(2a,a)知,顶点C在直线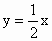 上. 上.
(2) 令阴影面积为S,则
∴ 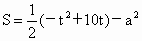
又∵点 C(2a,a)在直线PQ上∴ 2at-(2t-10)a=-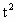 +l0t +l0t
∴ 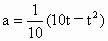
∴ 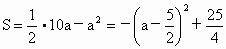
∴当 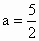 时, 时,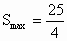 , ,
此时, A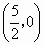 、B(5,0)、C 、B(5,0)、C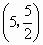 、D 、D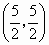
|
|
本题体现方程函数思想,用到待定系数法及解方程的知识. ①这是一道结论开放的探索性命题,通常假设结论是肯定的,若由此推导出的结果与已知条件和其他数学定理无矛盾,则结论是肯定性的,否则,结论就是否定的. ②最值问题转化为函数求最值. |


科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
t∈R,t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).问:①直线PQ是否能通过下面的点M(6,1),N(4,5);②在△OPQ内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.

(1)求证:顶点C一定在直线y=![]() x上.
x上.
(2)求下图中阴影部分面积的最大值,并求这时顶点A、B、C、D的坐标.
查看答案和解析>>
科目:高中数学 来源:天骄之路中学系列 读想用 高二数学(上) 题型:044
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
(1)问:直线PQ是否能通过下面的点M(6,1),N(4,5);
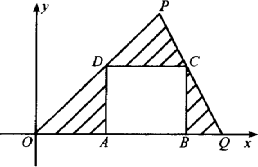
(2)在△OPQ内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在OP上.
①求证:顶点C一定在直线y=![]() x上;
x上;
②求如图中阴影部分面积的最大值,并求这时顶点A、B、C、D的坐标.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0),问:①直线PQ是否能通过点M(6,1)和N(4,5);②在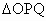 内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.
内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.
(1)求证:顶点C一定在直线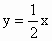 上;
上;
(2)求图中阴影部分面积的最大值,并求此时顶点A、B、C、D的坐标
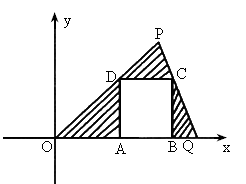
查看答案和解析>>
科目:高中数学 来源: 题型:
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
问:(1)直线PQ是否能通过下面的点M(6,1),N(4,5);
(2)在△OPQ内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.①求证:顶点C一定在直线![]() 上.
上.
②求下图中阴影部分面积的最大值,并求这时顶点A、B、C、D的坐标.w.w.w.k.s.5.u.c.o.m ![]()
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com