④
分析:①对sinA+cosA=

,两边同时平方可得整理可得,
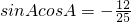
则有

②

•

<0?B为锐角,但不能肯定△ABC为锐角三角形;③由正弦定理可得
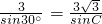
?
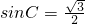
结合c>b 可得C>B=30°从而可得,当C=60°时A=90° 当 C=120°时,A=30°④由题意可得A,B,C不能为直角,钝角最多一个,故可设设A,B均为锐角,由tanA+tanB+tanC>0,结合三角形的内角和及两角和的正切公式,tanA+tanB>tan(A+B)?
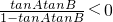
?tanAtanB>1
?tanA>cotB=tan(

)?A
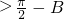
?

解答:①sinA+cosA=

,?
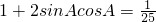
,
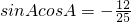
所以

①不能推出
②

•

<0?B为锐角,但不能肯定△ABC为锐角三角形
③由正弦定理可得
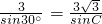
?
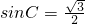
∵c>b∴C>B=30°
当C=60°时A=90° 当 C=120°时,A=30°③不能推出
④由题意可得A,B,C不能为直角,故可设设A,B均为锐角
tanA+tanB+tanC>0?tanA+tanB>tan(A+B)?
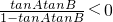
?tanAtanB>1
?tanA>cotB=tan(

)?A
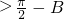
?

④为锐角三角形
故答案为:④
点评:本题以三角形的判断为平台,综合考查了同角平方关系,向量的夹角的概念,正弦定理及大边对大角,两角和的正切公式、三角形的内角和定理、正切函数的单调性.

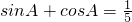 ②
② •
• <0
<0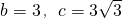 ,B=30°④tanA+tanB+tanC>0.
,B=30°④tanA+tanB+tanC>0. ,两边同时平方可得整理可得,
,两边同时平方可得整理可得,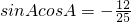 则有
则有
 •
• <0?B为锐角,但不能肯定△ABC为锐角三角形;③由正弦定理可得
<0?B为锐角,但不能肯定△ABC为锐角三角形;③由正弦定理可得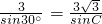 ?
?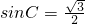 结合c>b 可得C>B=30°从而可得,当C=60°时A=90° 当 C=120°时,A=30°④由题意可得A,B,C不能为直角,钝角最多一个,故可设设A,B均为锐角,由tanA+tanB+tanC>0,结合三角形的内角和及两角和的正切公式,tanA+tanB>tan(A+B)?
结合c>b 可得C>B=30°从而可得,当C=60°时A=90° 当 C=120°时,A=30°④由题意可得A,B,C不能为直角,钝角最多一个,故可设设A,B均为锐角,由tanA+tanB+tanC>0,结合三角形的内角和及两角和的正切公式,tanA+tanB>tan(A+B)?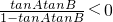 ?tanAtanB>1
?tanAtanB>1 )?A
)?A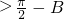 ?
?
 ,?
,?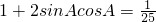 ,
,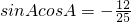 所以
所以 ①不能推出
①不能推出 •
• <0?B为锐角,但不能肯定△ABC为锐角三角形
<0?B为锐角,但不能肯定△ABC为锐角三角形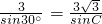 ?
?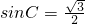 ∵c>b∴C>B=30°
∵c>b∴C>B=30°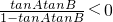 ?tanAtanB>1
?tanAtanB>1 )?A
)?A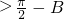 ?
? ④为锐角三角形
④为锐角三角形

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案