
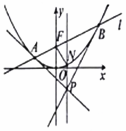
 我国唐代诗人王维诗云:“明月松间照,清泉石上流”,这里明月和清泉,都是自然景物,没有变,形容词“明”对“清”,名词“月”对“泉”,词性不变,其余各词均如此.变化中的不变性质,在文学和数学中都广泛存在.比如我们利用几何画板软件作出抛物线C:x2=y的图象(如图),过交点F作直线l交C于A、B两点,过A、B分别作C的切线,两切线交于点P,过点P作x轴的垂线交C于点N,拖动点B在C上运动,会发现$\frac{|NP|}{|NF|}$是一个定值,该定值是1.
我国唐代诗人王维诗云:“明月松间照,清泉石上流”,这里明月和清泉,都是自然景物,没有变,形容词“明”对“清”,名词“月”对“泉”,词性不变,其余各词均如此.变化中的不变性质,在文学和数学中都广泛存在.比如我们利用几何画板软件作出抛物线C:x2=y的图象(如图),过交点F作直线l交C于A、B两点,过A、B分别作C的切线,两切线交于点P,过点P作x轴的垂线交C于点N,拖动点B在C上运动,会发现$\frac{|NP|}{|NF|}$是一个定值,该定值是1. 分析 线段AB是过抛物线x2=y焦点F的弦,过A,B两点分别作此抛物线的切线,两切线相交于N点.N点在抛物线的准线上.根据抛物线的定义知:NF=NP,∴现$\frac{|NP|}{|NF|}$是一个定值1.
解答 解:线段AB是过抛物线x2=y焦点F的弦,过A,B两点分别作此抛物线的切线,两切线相交于N点.N点在抛物线的准线上.下面证明
证明:由抛物线x2=y,得其焦点坐标为F(0,$\frac{1}{4}$).
设A(x1,x12),B(x2,x22),
直线l:y=kx+$\frac{1}{4}$代入抛物线x2=y得:x2-kx-$\frac{1}{4}$=0.
∴x1x2=-$\frac{1}{4}$…①.
又抛物线方程为:y=x2,
求导得y′=2x,
∴抛物线过点A的切线的斜率为2x1,切线方程为y-x12=2x1(x-x1)…②
抛物线过点B的切线的斜率为2x2,切线方程为yx22-=2x2(x-x2)…③
由①②③得:y=-$\frac{1}{4}$.
∴P的轨迹方程是y=-$\frac{1}{4}$,即N在抛物线的准线上;
根据抛物线的定义知:NF=NP,∴$\frac{|NP|}{|NF|}$是一个定值1.
故答案为:1
点评 本题考查了抛物线的性质,对运算能力的要求比较高,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
 如图,将两块三角板拼在一起组成一个平面四边形ABCD,若$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R).则x+y=1+$\frac{4\sqrt{3}}{3}$.
如图,将两块三角板拼在一起组成一个平面四边形ABCD,若$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R).则x+y=1+$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既有最大值又有最小值 | B. | 有最大值没有最小值 | ||
| C. | 有最小值没有最大值 | D. | 既没有最大值也没有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com