
若数列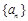 满足
满足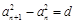 ,其中
,其中 为常数,则称数列
为常数,则称数列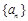 为等方差数列
为等方差数列
已知等方差数列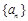 满足
满足 。
。
(Ⅰ)求数列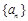 的通项公式;
的通项公式;
(Ⅱ)记 ,则当实数
,则当实数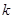 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的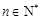 恒成立?请说明理由
恒成立?请说明理由
(Ⅰ)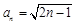 ;
;
(Ⅱ)当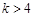 时,不等式
时,不等式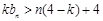 对于一切的
对于一切的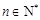 恒成立.
恒成立.
【解析】本试题主要考查了等方差数列的定义的理解和运用,涉及到求解数列的通项公式和数列解决不等式的恒成立问题的综合运用。
(1)根据数列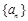 满足
满足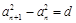 ,其中
,其中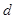 为常数,则称数列
为常数,则称数列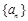 为等方差数列和
为等方差数列和 ,得到公差d,进而求解通项公式。
,得到公差d,进而求解通项公式。
(2)因为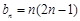 ,不等式
,不等式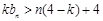 恒成立,
恒成立,
即 对于一切的
对于一切的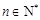 恒成立,运用分离参数法的思想得到证明。
恒成立,运用分离参数法的思想得到证明。
解:(Ⅰ)由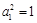 ,
,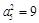 得,
得,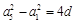 ,
,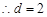 .…………………3分
.…………………3分
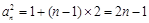 ,
,
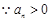 ,
,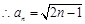 ,
,
数列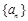 的通项公式为
的通项公式为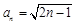 ;………………… 6分
;………………… 6分
(Ⅱ)解法一: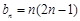 ,不等式
,不等式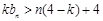 恒成立,
恒成立,
即 对于一切的
对于一切的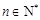 恒成立.
………………… 8分
恒成立.
………………… 8分
设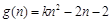 .
………………… 9分
.
………………… 9分
当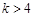 时,由于对称轴
时,由于对称轴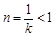 ,且
,且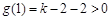
而函数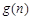 在
在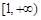 是增函数,………………… 10分
是增函数,………………… 10分
不等式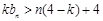 恒成立,
恒成立,
即当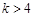 时,不等式
时,不等式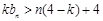 对于一切的
对于一切的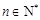 恒成立.
……………… 12分
恒成立.
……………… 12分
解法二: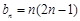 ,不等式
,不等式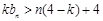 恒成立,
恒成立,
即 对于一切的
对于一切的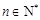 恒成立.
………………… 8分
恒成立.
………………… 8分
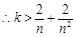 ………………… 9分
………………… 9分
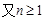 ,
,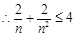 .………………… 10分
.………………… 10分
而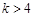
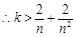 恒成立.
恒成立.
故当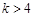 时,不等式
时,不等式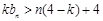 对于一切的
对于一切的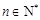 恒成立.
………………… 12分
恒成立.
………………… 12分


科目:高中数学 来源: 题型:
| an+2 |
| an+1 |
| an+1 |
| an |
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
| n•3n |
| 3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| sina |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4an-2 |
| an+1 |
| 146 |
| 65 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都外国语学校高三(上)11月月考数学试卷(解析版) 题型:填空题
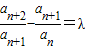 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都外国语学校高三(上)11月月考数学试卷(解析版) 题型:填空题
 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com