
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元).这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据y(单位:十亿元),绘制如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示
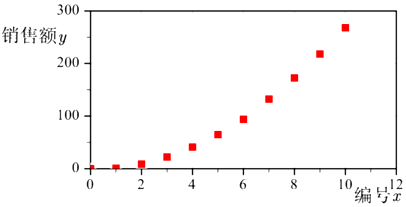
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及如表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
(3)把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考数据:![]()
|
|
|
|
|
|
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别
的斜率和截距的最小二乘估计公式分别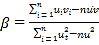 ,
,![]() .
.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)在散点图中,样本点并没有分布在某一个带状区域内,因此这两个变量不呈线性相关关系,则销售额![]() 关于
关于![]() 的回归方程类型;
的回归方程类型;
(2)令![]() ,则
,则![]() ,由最小二乘法得出其回归方程,并预测2020年天猫双十一销售额;
,由最小二乘法得出其回归方程,并预测2020年天猫双十一销售额;
(3)利用列举法以及古典概型概率公式计算概率即可.
(1)由散点图可知,![]() 适宜作为销售额
适宜作为销售额![]() 关于
关于![]() 的回归方程类型;
的回归方程类型;
(2)令![]() ,则
,则![]() .
.![]() ,
,![]()
 ,
,![]()
![]() ,则
,则![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,取
,取![]() ,得
,得![]() (十亿元).
(十亿元).
预测2020年天猫双十一销售额为324.7(十亿元);
(3)2010年到2019年这十年中“畅销年”有4年,其中“狂欢年”有2年.
从中任取2个,基本事件总数为![]() 共6个
共6个
至少取到一个“狂欢年”的事件数为![]() 共5个
共5个
则至少取到一个“狂欢年”的概率为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在宽为![]() 的路边安装路灯,灯柱
的路边安装路灯,灯柱![]() 高为
高为![]() ,灯杆
,灯杆![]() 是半径为
是半径为![]() 的圆
的圆![]() 的一段劣弧.路灯采用锥形灯罩,灯罩顶
的一段劣弧.路灯采用锥形灯罩,灯罩顶![]() 到路面的距离为
到路面的距离为![]() ,到灯柱所在直线的距离为
,到灯柱所在直线的距离为![]() .设
.设![]() 为灯罩轴线与路面的交点,圆心
为灯罩轴线与路面的交点,圆心![]() 在线段
在线段![]() 上.
上.
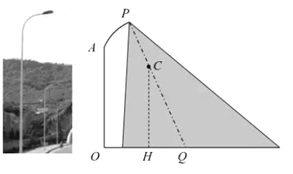
(1)当![]() 为何值时,点
为何值时,点![]() 恰好在路面中线上?
恰好在路面中线上?
(2)记圆心![]() 在路面上的射影为
在路面上的射影为![]() ,且
,且![]() 在线段
在线段![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,且以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,且以原点O为圆心,椭圆C的长半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的标准方程;
(2)已知动直线l过右焦点F,且与椭圆C交于A、B两点,已知Q点坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
性别 步数 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X﹣Y|,求E的分布列及数学期望.
附:K2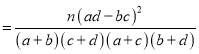 ,n=a+b+c+d.
,n=a+b+c+d.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com